还好这场没打 MD什么破题
n<=100000,m<=200000的图问从s点出发能否走奇数条边到一个没有出度的点。
直观的想法:做一个bfs,$f(i,0/1)$表示从$s$出发到$i$能否走奇数/偶数条边,搜出来,找一个$f(t,1)=1\ \ && \ \ chudu(t)=0$的点做终点。
如果找不到,就看能否走进一个环。
然后开始跳坑辣!(排名不分先后)
坑一:能否走进一个环,咋写?我先这样写的

mdzz,直接搜好像不靠谱。。老老实实写tarjan吧
坑二:最后构造答案,咋写?
法一:反向图再跑一次bfs,从起点开始跑,看一条边两端的点是否一个$f(i,1)=1$一个$f(j,0)=1$,能就走。然后挂了。
由于路上可能有一个偶环,为了不让人在里面死循环,我先判的一个点不经过超过两次。
然后有这个图:
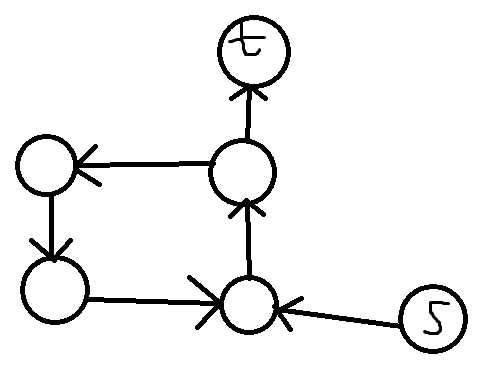
你xx在玩我!
坑三:
法二:zz吧直接bfs的时候记个前驱,从终点开始往前跑,跑到起点结束。嗯好像没啥毛病。
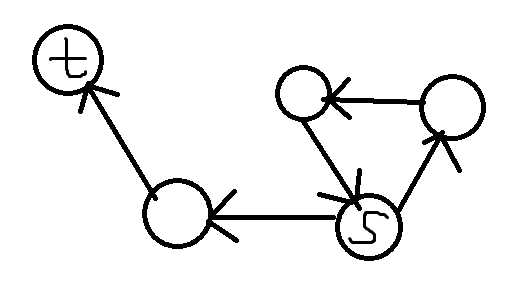
。。。。。。。。。。。。。。。
好吧往前跑的时候记一下奇数条边还是偶数,偶数就别停了。

1 //#include<iostream> 2 #include<cstring> 3 #include<cstdlib> 4 #include<cstdio> 5 //#include<map> 6 #include<math.h> 7 //#include<time.h> 8 //#include<complex> 9 #include<algorithm> 10 using namespace std; 11 12 int n,m,s; 13 #define maxn 200011 14 #define maxm 200011 15 struct Edge{int to,next;}; 16 struct Graph 17 { 18 Edge edge[maxm]; int first[maxn],le; bool du[maxn]; 19 Graph() {le=2;} 20 void in(int x,int y) {Edge &e=edge[le]; e.to=y; e.next=first[x]; first[x]=le++; du[x]=1;} 21 22 bool d[maxn],b[maxn],vis[maxn]; int pd[maxn],pb[maxn]; 23 int que[maxn],head,tail; 24 void sh(int s) 25 { 26 que[head=(tail=1)-1]=s; 27 d[s]=0; b[s]=1; vis[s]=1; 28 while (head!=tail) 29 { 30 int now=que[head++]; if (head==maxn) head=0; vis[now]=0; 31 for (int i=first[now];i;i=edge[i].next) 32 { 33 Edge &e=edge[i]; 34 if (d[e.to]==0 && b[now]) 35 { 36 d[e.to]=1; pd[e.to]=now; 37 if (!vis[e.to]) 38 { 39 vis[e.to]=1; 40 que[tail++]=e.to; 41 if (tail==maxn) tail=0; 42 } 43 } 44 if (b[e.to]==0 && d[now]) 45 { 46 b[e.to]=1; pb[e.to]=now; 47 if (!vis[e.to]) 48 { 49 vis[e.to]=1; 50 que[tail++]=e.to; 51 if (tail==maxn) tail=0; 52 } 53 } 54 } 55 } 56 } 57 58 int dfn[maxn],Time,low[maxn],sta[maxn],top; bool insta[maxn]; 59 bool dfs(int x) 60 { 61 low[x]=dfn[x]=++Time; 62 sta[++top]=x; insta[x]=1; 63 for (int i=first[x];i;i=edge[i].next) 64 { 65 Edge &e=edge[i]; 66 if (!dfn[e.to]) 67 { 68 if (dfs(e.to)) return 1; 69 low[x]=min(low[x],low[e.to]); 70 } 71 else if (insta[e.to]) low[x]=min(low[x],dfn[e.to]); 72 } 73 if (dfn[x]==low[x]) 74 { 75 if (sta[top]!=x) return 1; 76 top--; insta[x]=0; 77 } 78 return 0; 79 } 80 bool roll(int s) {Time=top=0; return dfs(s);} 81 }g,fg; 82 83 int ans[maxn*10],lans=0; 84 int main() 85 { 86 scanf("%d%d",&n,&m); 87 for (int i=1,x,y;i<=n;i++) 88 { 89 scanf("%d",&x); 90 for (int j=1;j<=x;j++) scanf("%d",&y),g.in(i,y),fg.in(y,i); 91 } 92 int s,t=0; 93 scanf("%d",&s); 94 g.sh(s); 95 for (int i=1;i<=n;i++) if (!g.du[i] && g.d[i]) {t=i; break;} 96 if (t) 97 { 98 puts("Win"); 99 for (int x=t,sb=0;x!=s || ((lans&1)==0);sb^=1) 100 { 101 ans[++lans]=x; 102 if (sb) x=g.pb[x]; 103 else x=g.pd[x]; 104 } 105 ans[++lans]=s; 106 for (int i=lans;i;i--) printf("%d ",ans[i]); 107 } 108 else 109 { 110 if (g.roll(s)) puts("Draw"); 111 else puts("Lose"); 112 } 113 return 0; 114 }

