欧拉回路与欧拉路径
如果图G中的一个路径包括每个边恰好一次,则该路径称为欧拉路径(欧拉通路)。
如果一个回路是欧拉路径,则称为欧拉回路(Euler circuit)。
说的直白点,欧拉回路就是从一个点出发,经过每一条边恰好一次,最后能回到这个点的路径
例如下图中的红色路径组成了一个欧拉回路
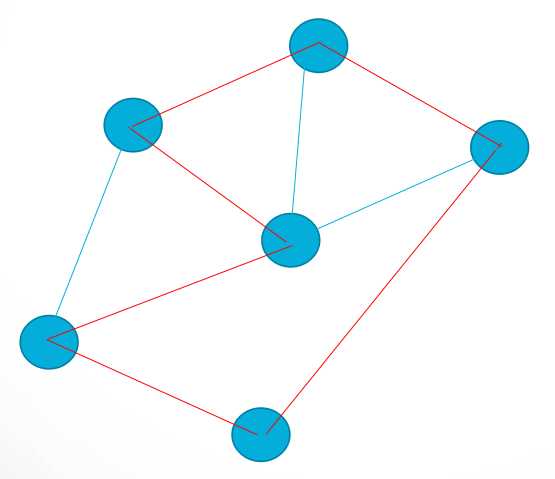
存在条件
欧拉回路的充要条件
无向图:所有点的度数都为偶数
有向图:所有点的入度都等于出度
欧拉路径的充要条件
无向图:除两点(起点与终点)外其余所有点的度数都为偶数
有向图:除两点(起点入度\(+1\)=出度,终点入度\(-1\)等于出度)外,其余所有点的入度等于出度
判断方法
利用并查集判断
若给出的图满足欧拉回路/欧拉路径的重要条件且并查集成功合并的 次数\(>=\)点数\(-1\),则证明含有欧拉回路/欧拉路径
欧拉路径:洛谷P1333
欧拉回路:HDU 1878
dfs
如果要求输出方案,那么只能用dfs
拓展
这里再补充一种两笔画问题
解决方法比较简单
有解当且仅当度数为奇数的点不超过4个。
将其中两个点加一条边后求欧拉路径,在这条边处断开变成两条路径即可。
时间复杂度\(O(m)\)
