题意略。
这个题目最关键的是在于计算球冠的体积。令球冠体积为V。
我们可以用祖暅原理来计算V,
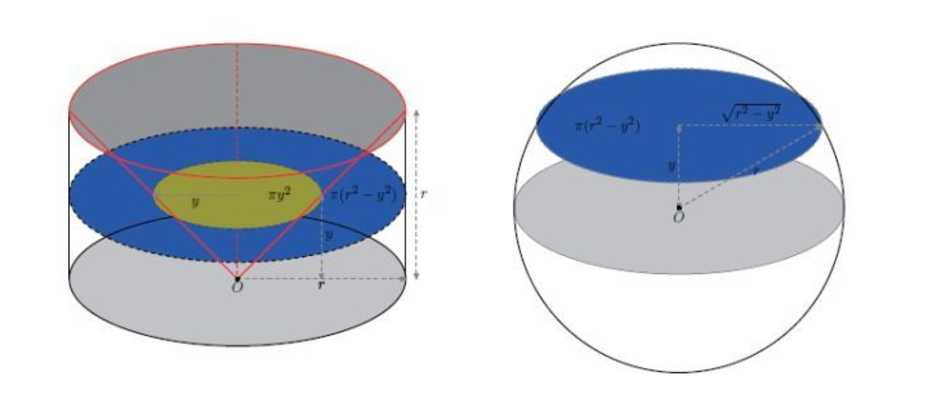
这里,可以看出,球冠的体积等于左图的上半个圆柱减去那个倒扣的圆台。
祖暅原理:界于两个平行平面之间的两个立体,被任一平行于这两个平面的平面所截,如果两个截面的面积相等,则这两个立体的体积相等。
V = Pi * r^2 * (r - y) - V(圆台)
本题分为五种情况来讨论:
1.球完全内含于圆柱。
2.球左右凸出圆柱,但是上下不突出。
3.球左右不凸出圆柱,但是上下突出圆柱。
4.球上下左右均凸出,但是尚未包含圆柱。
5.球包含圆柱。
#include<bits/stdc++.h> #define Pi acos(-1.0) using namespace std; double R,HR,HZ; int main(){ while(scanf("%lf%lf%lf",&R,&HR,&HZ) == 3){ double part1,part2; double v1 = Pi * R * R * R * 4.0 / 3.0; double v2 = Pi * HR * HR * HZ * 2; if(R <= HR && R <= HZ){ part1 = v1; part2 = v2; } else if(R <= HR && R > HZ){ double add = Pi * R * R * (R - HZ) - 1.0 / 3.0 * Pi * (R - HZ) * (HZ * HZ + R * R + HZ * R); part1 = v1 - 2 * add; part2 = v2 + 2 * add; } else if(R > HR && R <= HZ){ double d = sqrt(R * R - HR * HR); double add = Pi * R * R * (R - d) - 1.0 / 3.0 * Pi * (R - d) * (d * d + R * R + d * R); add = 2.0 / 3 * Pi * R * R * R - add; add *= 2; add -= Pi * HR * HR * 2 * d; part1 = v1 - add; part2 = v2 + add; } else if(R > HR && R > HZ && R < sqrt(HR * HR + HZ * HZ)){ double add1 = Pi * R * R * (R - HZ) - 1.0 / 3.0 * Pi * (R - HZ) * (HZ * HZ + R * R + HZ * R); double d = sqrt(R * R - HR * HR); double add2 = Pi * R * R * (R - d) - 1.0 / 3.0 * Pi * (R - d) * (d * d + R * R + d * R); add2 = 2.0 / 3.0 * Pi * R * R * R - add2; add2 *= 2; add2 -= Pi * HR * HR * 2 * d; part1 = v1 - 2 * add1 - add2; part2 = v2 + 2 * add1 + add2; } else if(R >= sqrt(HR * HR + HZ * HZ)){ part1 = v2; part2 = v1; } printf("%lf\n",part1 / part2); } return 0; }
