title: 博弈论 斯坦福game theory stanford week 1-2
tags: note
notebook: 6- 英文课程-15-game theory
---
博弈论 斯坦福game theory stanford week 1-2
贪婪代理
贪婪代理是什么?:
- 他们并不是想要伤害其他人或者只考虑自己
- 只是他们的行为基于对于世界上的情况的描述
这种代理有一个独特的方法
- 在不同的选择中量化偏好程度。
- 解释不确定的影响
- 决策理论相关:最大化期望效果
定义博弈
players: 决策者,就是决定的做出者
action:就是行为,也就是决策者做出的行动
payoff:收益,也就是决策可以收到的利益
normal form:一般形式,矩阵形式和策略形式来讨论的一种进行决策的形式,以列表表示
extensive form:广泛形式,树形表示
如下图的形式:
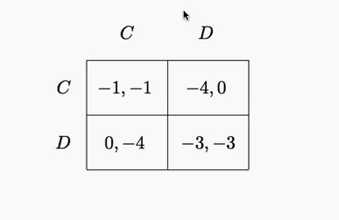
就是一个矩阵形式
一个大的博弈参与者可以有很多
行为也可以有很多
如果我们能够定义以上的各种变量,也就可以定义一个博弈
例子
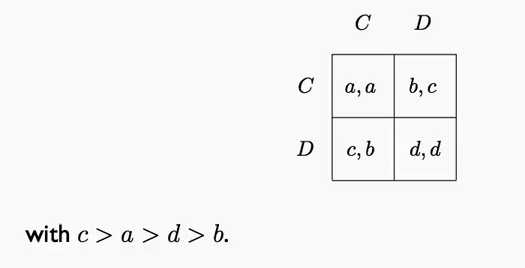
如图所示,是一个违反直觉的博弈的例子,我们看到a>b>c>d
如果两个人选择c,都会得到较大的收益,但是却因为害怕对方选择D而让自己的收益下降,都选择了D,都获得了较小的收益。
从而引出博弈的种类:
零和博弈,就是决策造成的利益总和不发生改变
合作的基础
我们从博弈论中可以对合作的基础进行简单的分析,合作者拥有相同的利益,
不过有些场合时不能合作的
纳什均衡
举个例子,如果大家进行选美比赛,你要怎么选才能成功选中,结果是,你不要选你认为最漂亮的,而是要选你认为大叫都会选的。
那么会发生什么呢?
- 我们定义:每一个游戏者都会被编号1-100
- the player who name the integer closest to two thirds of the average integer wins a prize, the other players get nothing.
- 也就是说最接近平均数2/3的玩家获得奖品,
- ties are broken uniformly at random
所有的关系都是随机的
关于这一点,我们来做一个“选美比赛”博弈实验。博弈程序如下:一群受试者在0~100之间选一个整数,选的数字最接近猜测平均数的2/3为赢家,可获得奖品10万元。当然,每个人的思维逻辑是不同的,但一般地,以下两种是大多数受试者面对这个博弈情形的基本思维方式。
【思维一:最大平均数思维】由于67是100的2/3的最大平均数,因此,博弈方应该选择比67小的数字而取得占优策略,所有博弈方的选择范围缩小到[0,67]。给定这个共同知识,由于44是67的2/3的最大平均数,因此,博弈方就应该选择比44小的数字而取得占优策略,所有博弈方的选择范围缩小到[0,44]。给定这个共同知识,由于29是44的2/3的最大平均数,因此,博弈方就应该选择比29小的数字而取得占优策略,所有博弈方的选择范围又缩小到[0,29]都会小于29。随后在被缩小到[0,20]…… 以此类推,那么就可以得到唯一的纳什均衡0。
【思维二:随机平均数思维】假设人们的选择是随机的,那么,在[0,100]中选择的中位数或平均数就是50,因而33就成为最佳选择;但如果给定他人都选择33的情况下, 22又成为更佳的选择;……这样循环下去,最后的结果还是0。
