一、资料分析——增长量/率和同/环比
1、增长量和增长率
思考下面三个问题:
- 今年产量为M比去年产量N多多少?
- 今年产量比去年产量增长了多少百分比?
- 去年产量比今年产量减少了多少百分比?
对于M比N这种问题,我们一般将“比”字后面的M称为基期,“比”字前面的N称为现期。
所以:
- 增长量 = 现期 - 基期
- 增长率 = 增长量 / 基期
2、同比和环比
同比和环比的都是求增长率,区别在于基期不同:
- 同比的基期:上个时间段的同期
- 环比的基期:上期
比如2018年1月产量为M,同比增长率10%,环比下降率5%。相当于2018年4月产量为M,比2017年4月增长了10%,比2017年12月增长了5%。
二、资料分析——易混淆的三个点
1、百分数和百分点
思考这样一个问题:
- 10%比6%增加了多少百分数?
如果你答4%,那么就大错特错了,思考同样的问题“今年产量M比去年产量N增长了多少百分比?”这个问题很明显是求增长率的,所以答案应该 = (10%-6%)/6% = 66.6%。但是如果4%换一个说法也可以作为答案,即“10%比6%增加了4%个百分点”。
所以百分数是求增长率,而百分比是求两个百分数之间的差值。以上数字
2、倍数和翻番
我们常说的倍数就是几倍的意思,而翻一番是指两倍的意思,所以翻两番就是四倍的意思。以此类推,
- 翻n番 = 2^n倍。
3、平均数和中位数
三、资料分析——比重和指数
- 比重是指部分占整体的百分比。
- 指数是指任何两个数字对比形成的相对数都可以称为指数。例如一串数字:50、133、154、180
假设这是第一季度的用电量,求后三个月份的用电增长率。我们可以很容易使用公式 = 本月用电量增量 / 上月用电量。这是数字相对简单的情况,如果很复杂或很多时我们就不容易计算了,所以统计学者考虑到:可以将按某种比例换算成相对数,以此便于计算数据间的比值,这样就得到了一个指数表:100、266、308、360。这样计算就变得简单明了,基本可以口算得到,这就是指数的作用。
四、数学运算——必考的几个点
1、行程问题
假设同一时间出发,有以下两种情况:
- 相遇问题:路程和 = 速度和 × 相遇时间
- 追及问题:路程差 = 速度差 × 追及时间
2、工程问题
- 工作总量 = 工作效率 × 工作时间
- 合作效率 = 个体效率之和
3、浓度
- 浓度是指单位溶液中所含溶质的量。(这里量可以是质量,也可以是体积)。
- 公式:浓度 = (溶质 / 溶液)×100% = 溶质 / (溶质+溶剂)。
4、集合
- 并集
- 交集
- 全集和补集
五、行程问题必知的几个点
1、反比
基本公式为S = vt。追及问题中则有:v1/v2 = t2/t1。这样有时会方便计算。
2、流水行船
- 顺流而下的速度 = V船 + V水
- 逆流而上的速度 = V船 - V水
3、火车过桥
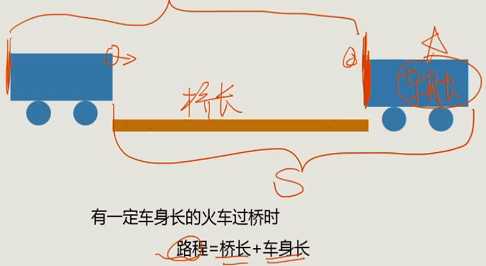
4、时钟问题
- V时针 = 30度/时 = 0.5度/分钟
- V分钟 = 6度/分钟
5、发车问题
设发车间隔为t,那么两车间隔 = V车 × t
六、“设1法”的原理
1、原理
例题:假设甲做完一项任务需要6天,乙做完同样的任务需要3天,那么两人一起工作需要几天?
很明显这是一个工程问题,那么工作时间 = 工作总量/工作效率。现在我们不知道工作总量是多少,一般我们会假设为1,那么工作时间 = 1 / (1/6+1/3)= 2天,这是因为无论我们将工作总量设为多少,比如m来计算都不会影响计算结果。
所以“设1法”的原理其实就是一个不影响答案的未知数我们可以设置为1来方便计算。
2、改进
除了设置为1,其实我们可以设置为任意数,那么为了方便计算,我们应该尽量设置为方便计算的数,比如:
例题:一项工程,甲完成需要6天,乙完成需要4天,那么甲乙一起工作需要几天?
同样的,我们可以不设置工程量为1,我们可以设置为6和4的公倍数,这样会方便计算,所以需要天数 = 12/(2+3) = 12/5 = 2.4天。
七、整除规律
1、能被2、3(9)、5整除的数字规律
- 能被2整除的数字一定是偶数
- 能被5整除的数个位一定是0或5
- 各个位置上的数字之和能被3(9)整除的数就能被3整除
2、能被2、4、8或5、25、125整除的数字规律
- 2(5):个位数字能被2(5)整除
- 4(25):最后两位数字能被4(25)整除
- 8(125):末三位数字能被8(125)整除
3、能被7、11、13整除的数字规律
- 末三位与末三位之前的数字之差能被7、11、13整除。比如1122的末三位是122,之前的数字为1,差为121能被11整除,那么1122也能被11整除。
4、相关例题
例1:某班学生在操场上做操,人数在90~110之间,若过排成3排则不多不少,排成完整的5排少2人,排成完整的7排少4人,那么学生人数为?()
A、102 B、98 C、104 D、108
分析:首先能被3着整除,根据整除特点直接排出B和C。排成5排少2人,那么这个数字+2就能被5整除,能被5整除的数字各位是0或5,那么学生人数各位就是8或3,排除A,直接选D。
八、数列及其和
1、等差数列
计算公式:
但我们一般很少使用这个公式求和:
- 使用平均数法求和:Sn = n*平均数 = (a1+an)n / 2
- 常见的等差数列:自然数列,公差为1的数列。
2、等比数列
九、最小公倍数和同余定理
1、最小公倍数
例1:一个数除以32、36、48都余15,那么这个数最小为()
A、289 B、297 C、303 D、363
解析:其实0可以整除这些数,但答案没有15,我们接着看,假设这个数为x,那么x+15都能被32、36、48整除,要求最小数字,即求最小公倍数,所以这三个数的最小公倍数 = x+15即可求出x。
例2:两个数的公约数为2,公倍数为1344,一个数为42,那么另一个数为?()
A、52 B、54 C、62 D、64
解析:其实有一个规律:
- 两个数的乘积 = 最大公约数 × 最小公倍数
所以答案很简单就可以计算得到 = 2×1344/42 = 64。
2、同余定理
- 余同取余
如果一个数的除以其他数的得到的余数都相同,那么这个数可能为 = 这些除数的最小公倍数×n + 约数
例:一个数除以2余1,除以3余1,除以7也余1,那么这个数可能为:
A、41 B、42 C、85 D、84
解析:2、3、7的最小公倍数为42,这个数可能为:42n + 1,选项中只有C符合 - 差同减差
如果一个数除以其他数得到的余数,对应的除数和余数差值d相同,那么这个数就可能为 = 这些除数的最小公倍数×n - 差值d
例:一个数除以3余2,除以4余3,除以5余4,那么这个数可能为()
解析:3,4,5的最小公倍数为60,上述除数和余的差都为1,所以这个数可能为:60n - 1 - 和同加和
如果一个数除以其他数得到的余数,对应的除数和余数和m相同,那么这个数就可能为 = 这些除数的最小公倍数×n + 和m
例:一个数除以4余3,除以5余2,除以6余1,那么这个数可能为()
解析:4、5、6的最小公倍数为60,余数和除数之和都为7,那么这个数可能为 = 60n + 7。
十、排列组合
1、公式
2、两个基本原则
- 不同的问题要分类相加
- 不同的步骤要分步相乘
例:A点到B点有几种出行方式和路线先选择?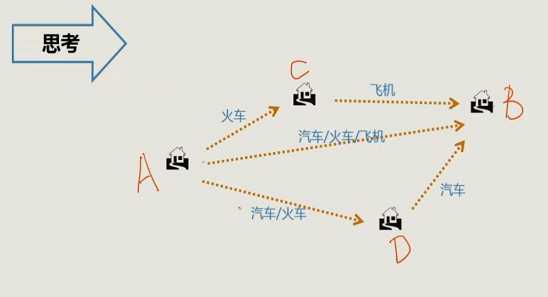
解析:A到B首先有三条线路,这是分类相加;每条线路又可以选择不同的出行方式,这是分步相乘。
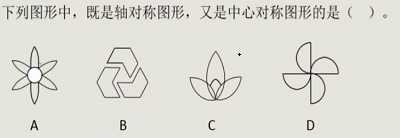
十一、图形推理——对称
1、概念
- 沿着某一直线进行对折能够完全重合的图形称为轴对称图形。
- 沿着某一个点旋转180度后能和旋转前完全重合的图形称为中心对称图形。
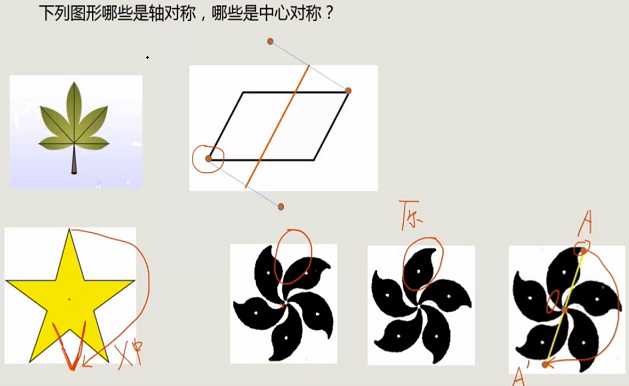
2、判断是轴对称还是中心对称

十二、图形推理——旋转和翻转
1、概念
- 旋转是图形绕某一点的平面转动。上面说到的中心对称图形就可以旋转180度而重合。
- 翻转是图像以某一直线进行空间转动。上面说到的轴对称图形中折叠就是翻转90度的意思。
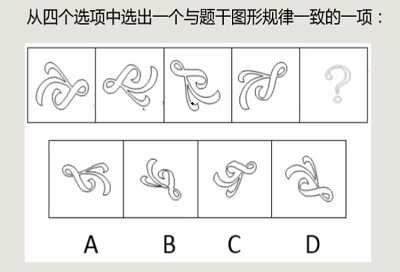
2、判断是旋转还是翻转
- 时针法:任意找三点画弧线,如果比较的图像旋转方向一致就是旋转,反之为翻转。
3、判断旋转了几度
- 箭头法:
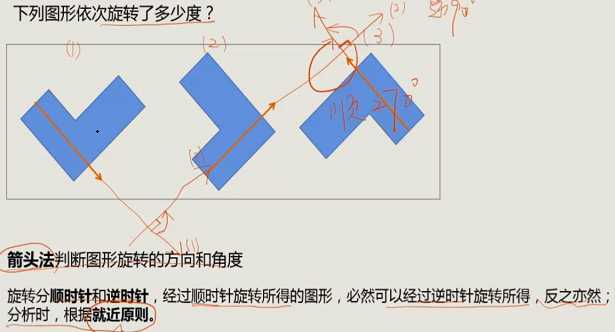
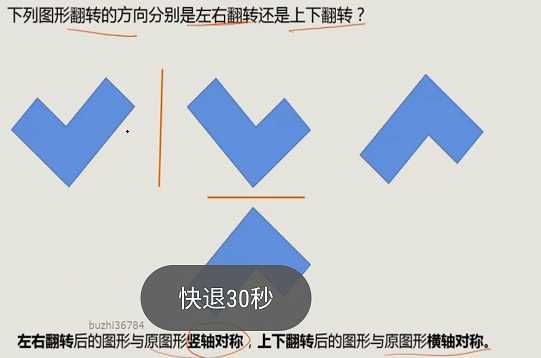
4、判断是上下翻转还是左右翻转