1 朴素贝叶斯法的学习与分类
Naive Bayes是基于贝叶斯定理和特征条件独立的假设的分类方法。对于给定的训练数据,首先基于特征条件独立学习输入和输出的联合概率分布,然后基于此模型,对给定的输入x利用贝叶斯定理求出后验概率最大的y。
1.1 基本原理
这里一张手写推导:

而这个P(ck|X=x)甚至可以是频率来估计。看下节部分。
2 参数估计
2.1 极大似然估计
先验概率P(Y=ck)的极大似然估计:
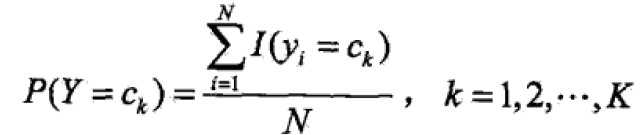
条件概率极大似然估计:

2.2 算法

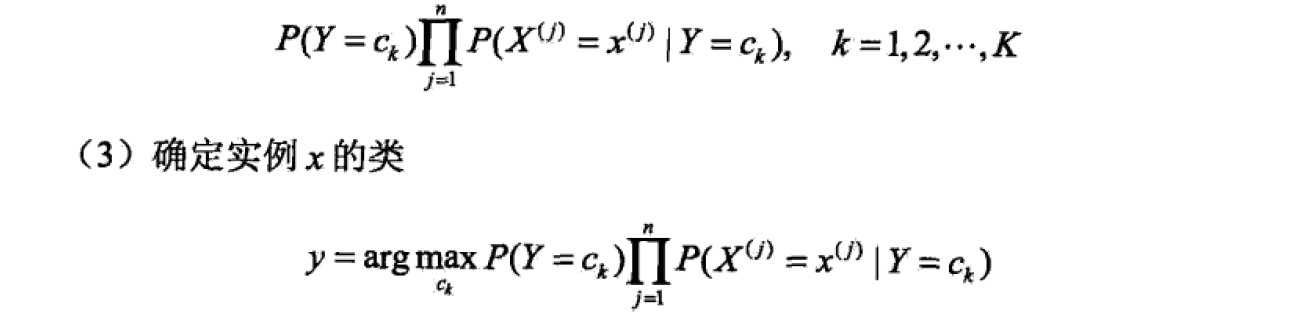
2.3 贝叶斯估计
贝叶斯估计解决的问题:极大似然估计可能会出现所要估计的概率值为0的情况,使得后验概率出现偏差。
条件概率的贝叶斯估计是:
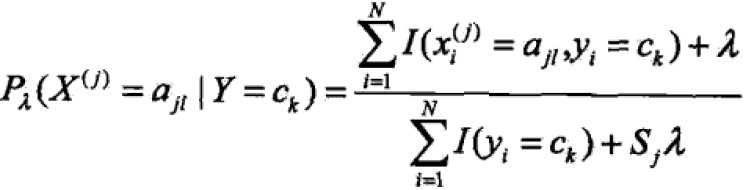
lambda>=0,相当于极大似然估计的每一个变量加上一个lambda,为0就是极大似然估计,常用值为1,这时称为拉普拉斯平滑(Laplace smoothing)。
证明其仍然为概率:
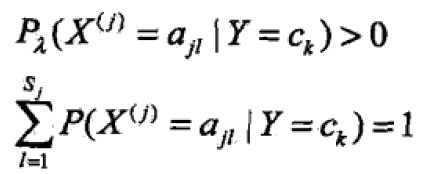
先验概率的贝叶斯估计为:
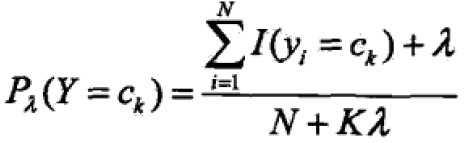
其中K是集合y中元素的个数,lambda是在Sigma之外的,不在连加符号内。
注意:Naive Bayes method是从训练数据学得P(X,Y)【P由P(X|Y)*P(Y)而得】生成的方法,是生成模型,有一个强假设:条件独立性。
