题意:给一个数字串,求不可重叠的相似子串,两个子串$a,b$相似的定义是$a_i-b_i$都相等
昨晚二爷讲课,去膜拜一发,学了一下不知道学了多少次也没懂的后缀数组
后缀数组能将字符串$S$的所有后缀$S_{i\cdots n}=\text{Suffix}(i)$排序,$sa_i$表示排第$i$名的后缀的开头下标,$rank_i$表示$\text{Suffix}(i)$的排名,$height_i$表示排第$i$名的后缀和排第$i-1$名的后缀的最长公共前缀长度
考虑用倍增求$rank_i$,一开始把所有长度为$1$的字符串排序,然后排序长度为$2$的字符串,以此类推
假设当前要排所有长度为$L$的字符串,因为我们已经知道了所有长度为$\dfrac L2$的字符串的相对大小,所以我们把每个长度为$L$的字符串看成由两个长度为$\dfrac L2$的字符串拼起来的东西,相当于用(长度为$\dfrac L2$的字符串的相对排名)构成的二元组来表示每一个长度为$L$的字符串
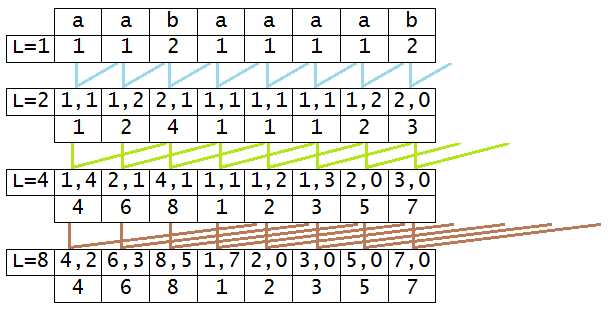
原理很简单,就是用长度为$\dfrac L2$的字符串之间的关系得出长度为$L$之间的字符串的关系
容易看出当$L=1$时字符串大小就是字母大小,之后每次用上一次得出的$rank$组成二元组并排序
注意到我们是对$rank$组成的二元组排序,这意味着被排序的数$\leq n$,所以我们可以使用计数排序,代码挺好写的
int cnt[N],tmp[N];
void sort(int*x){
int i,m=0;
for(i=1;i<=n;i++){
m=max(m,x[i]);
cnt[x[i]]++;
}
for(i=1;i<=m;i++)x[i]+=x[i-1];
for(i=n;i>0;i--)tmp[cnt[x[i]]--]=x[i];
for(i=1;i<=n;i++)x[i]=tmp[i];
}
计数排序的原理是统计“有多少个数小于等于这个数”,这里的自减符号用于处理元素相同的情况,倒过来处理保证了相等元素之间的相对顺序不会改变(每处理完一个元素,下次碰到这个元素时它的下标已经减去了$1$)
对二元组的排序也容易解决,先对第二维排序,再对第一维排序(因为计数排序是稳定排序,当排完后第一维相等的连续段的第二维是有序的)
于是我们成功求出了$rank_i$,那么$sa_i$也易于求得
我们还要求$height_i$,有一个关于它的结论是$height_{rank_i}\geq height_{rank_{i-1}}-1$,证明如下(来自许智磊的论文)
以下证明比较绕,请熟悉$sa,rank,height$的概念再看证明
当$height_{rank_{i-1}}\leq1$,显然成立
当$height_{rank_{i-1}}\geq2$,先证一堆奇奇怪怪的东西
设$lcp(i,j)=lcp(\text{Suffix}(sa_i),\text{Suffix}(sa_j))(i\leq j)$,它等价于$lcp(\text{Suffix}({sa_{i\cdots j}}))$
因为更多串取最长公共前缀不会让答案变大,所以如果$k\geq j\geq i$,那么$lcp(k,j)\geq lcp(k,i)$
设$k=sa_{rank_{i-1}-1}$,即$\text{Suffix}(k)$是$\text{Suffix}(i-1)$的前一位
根据$lcp(\text{Suffix}(k),\text{Suffix}(i-1))=height_{rank_{i-1}}\geq2$,两边同时向右偏移$1$位,最长公共前缀$-1$,所以$lcp(\text{Suffix}(k+1),\text{Suffix}(i))=height_{rank_{i-1}}-1$
因为$rank_{k}\lt rank_{i-1}$且$height_{rank_{i-1}}\geq2$,所以不等式两边所代表的后缀第一位相同,右移一位不影响比较结果,推出$rank_{k+1}\lt rank_i$,也就是$rank_{k+1}\leq rank_i-1$
因为$rank_i\geq rank_i-1\geq rank_{k+1}$,所以$lcp(rank_i,rank_i-1)\geq lcp(rank_i,rank_{k+1})=lcp(\text{Suffix}(i),\text{Suffix}(k+1))=height_{rank_{i-1}}-1$
最后,$height_{rank_i}=lcp(rank_i,rank_i-1)\geq height_{rank_{i-1}}-1$,于是就证完了
如果按$height_{rank_{1\cdots n}}$这样的顺序来求,那么它每次先$-1$,然后就只可能增加,这保证了整个求$height$的过程是$O(n)$的
算$height_i$的代码一定要记好,考场上没时间来证这种鬼定理
所以我们求出了后缀数组中用处最大的东西:$height_i$,下面用它做题
题目说“相似”,假如对原序列差分,那么问题就变成了不可重叠最长重复子串
考虑二分,假设当前二分的答案是$k$,如果存在$[l,r]$使任意$i\in[l,r]$都有$height_i\geq k$,那么这些后缀的$lcp$长度就$\geq k$,我们可以贪心地选取两个相距最远的后缀,也就是说如果$\max\left\{sa_{l\cdots r}\right\}-\min\left\{sa_{l\cdots r}\right\}\geq k$,那么就存在两个不重叠的长度为$k$的子串
因为差分了,所以最后答案应该$+1$
于是这题就做完了,唉终于填了一个看上去不可填的坑...
为什么我写的后缀数组常数这么鬼大>_<
#include<stdio.h>
#include<string.h>
int s[100010],rk[200010],sa[100010],cnt[100010],id[100010],height[100010],n;
struct pr{
int c[2],id;
pr(int a=0,int b=0,int d=0){c[0]=a;c[1]=b;id=d;}
}p[100010],q[100010];
bool operator!=(pr a,pr b){return(a.c[0]!=b.c[0])||(a.c[1]!=b.c[1]);}
int max(int a,int b){return a>b?a:b;}
int min(int a,int b){return a<b?a:b;}
void sort(int f){
int i,m;
memset(cnt,0,sizeof(cnt));
m=0;
for(i=1;i<=n;i++){
cnt[p[i].c[f]]++;
m=max(m,p[i].c[f]);
}
for(i=1;i<=m;i++)cnt[i]+=cnt[i-1];
for(i=n;i>0;i--)q[cnt[p[i].c[f]]--]=p[i];
for(i=1;i<=n;i++)p[i]=q[i];
}
void suf(){
int i,l,m;
memset(rk,0,sizeof(rk));
for(i=1;i<=n;i++)rk[i]=s[i];
for(l=1;l<=n;l<<=1){
for(i=1;i<=n;i++)p[i]=pr(rk[i],rk[i+l],i);
sort(1);
sort(0);
m=0;
for(i=1;i<=n;i++){
if(p[i]!=p[i-1])m++;
rk[p[i].id]=m;
}
}
for(i=1;i<=n;i++)sa[rk[i]]=i;
l=0;
for(i=1;i<=n;i++){
if(l)l--;
while(s[i+l]==s[sa[rk[i]-1]+l])l++;
height[rk[i]]=l;
}
}
bool check(int k){
int i,mx,mn;
for(i=1;i<=n;i++){
if(height[i]>=k){
mx=max(mx,max(sa[i-1],sa[i]));
mn=min(mn,min(sa[i-1],sa[i]));
}else{
mx=-1;
mn=n;
}
if(mx-mn>=k)return 1;
}
return 0;
}
int main(){
int i,l,r,mid,ans;
while(1){
scanf("%d",&n);
if(n==0)break;
for(i=1;i<=n;i++)scanf("%d",s+i);
n--;
for(i=1;i<=n;i++)s[i]=s[i+1]-s[i]+88;
suf();
l=1;
r=n>>1;
ans=0;
while(l<=r){
mid=(l+r)>>1;
if(check(mid)){
ans=mid;
l=mid+1;
}else
r=mid-1;
}
printf("%d\n",(ans<4)?0:(ans+1));
}
}
