望得分:100+100+100
实际得分:100+100+100
Problem 1 晨跑(running.cpp/c/pas)
【题目描述】
为了响应学校的号召,模范好学生王队长决定晨跑。不过由于种种原因,每
天都早起去跑步不太现实,所以王队长决定每 a 天晨跑一次。换句话说,假如王
队长某天早起去跑了步,之后他会休息 a-1 天,然后第 a 天继续去晨跑,并以此
类推。
王队长的好朋友小钦和小针深受王队长坚持锻炼的鼓舞, 并决定自己也要坚
持晨跑。小钦决定每 b 天早起跑步一次,而小针决定每 c 天早起跑步一次。
某天早晨,王队长、小钦和小针在早起跑步时相遇了,他们非常激动、相互
鼓励,共同完成了一次完美的晨跑。
为了表述方便,我们把三位同学相遇的这天记为第 0 天,他们想知道,下一
次三人在跑步时相遇是第几天。由于三位同学都不会算,所以希望由你来告诉他
们答案。
【输入格式】
输入文件 running.in
输入共一行,包含三个正整数 a,b,c,表示王队长每隔 a 天晨跑一次、小钦
每隔 b 天晨跑一次且小针每隔 c 天晨跑一次。
【输出格式】
输出文件 running.out
输出共一行,包含一个正整数 x,表示三位同学下次将在第 x 天相遇。
【样例输入】
2 3 5
【样例输出】
30
【数据范围】
对于 30%的数据 1<=a,b,c<=100
对于 50%的数据 1<=a,b,c<=1000
对于 100%的数据 1<=a,b,c<=1000000
solution: 很明显,答案就是$\lcm (a,b,c)$,只需要求出来两两之间的$\gcd$,然后套用一下$\lcm$的公式就行了。
我们有:
\begin{aligned}
\lcm (a,b)=\frac{ab}{\gcd(a,b)}\\
\lcm (a,b,c)=\lcm(\lcm(a,b),c)
\end{aligned}
问题得解。
#include <cstdio>
using namespace std;
typedef long long ll;
ll a,b,c;
inline ll gcd(ll a,ll b){return !b?a:gcd(b,a%b);}
inline ll lcm(ll a,ll b){return a*b/gcd(a,b);}
inline ll lcm(ll a,ll b,ll c){return lcm(lcm(a,b),c);}
int main()
{
#ifndef LOCAL
freopen("running.in","r",stdin);
freopen("running.out","w",stdout);
#endif
scanf("%lld%lld%lld",&a,&b,&c);
printf("%lld\n",lcm(a,b,c));
fclose(stdin);
fclose(stdout);
return 0;
}
Problem 2 货物运输(goods.cpp/c/pas)
【题目描述】
在一片苍茫的大海上,有 n 座岛屿,岛屿与岛屿之间由桥梁连接,所有的岛
屿刚好被桥梁连接成一个树形结构,即共 n-1 架桥梁,且从任何一座岛屿出发都
能到达其他任何一座岛屿。
第 i 座桥梁有一个承重量 wi, 表示该桥梁一次性最多通过重量为 wi 的货物。
现在有 m 个货物运输路线,第 i 个路线要从岛屿 xi 出发到达岛屿 yi。为了
最大化利益,你需要求出在不超过路线上任何一架桥梁的承重量的基础上,每个
路线最多运输重量为多少货物。
【输入格式】
输入文件 goods.in
第一行为两个整数 n,m。
接下来 n-1 行,每行三个整数 x,y,w,表示有一座承重量为 w 的桥梁连接岛
屿 x 和 y。
接下来 m 行,每行两个整数 x,y,表示有一条从岛屿 x 出发到达岛屿 y 的路
线,保证 x≠y。
【输出格式】
输出文件 goods.out
输出共 m 行,每行一个整数,第 i 个整数表示第 i 条路线的最大重量。
【样例输入】
6 5
1 2 2
2 3 5
2 4 2
2 5 3
5 6 1
2 4
6 2
1 3
3 5
1 6
【样例输出】
2
1
2
3
1
【样例解释】
岛屿间连接情况如图所示:
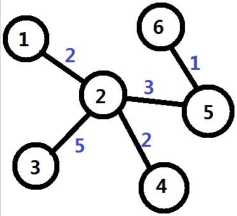
2,4 间只有一架桥,该路线最大运输重量为 2
6,2 间有两架桥,承重分别为 3 和 1,该路线最大运输重量为 1
剩余询问不再作解释
【数据范围】
对于 50%的数据 n,m<=2000
对于 100%的数据 n,m<=100000,w<=10^9
solution: NOIp2013 货车运输弱化版。给定一棵树,求一下LCA,在求LCA的时候顺便维护一下路径上的最小值(ST表),然后倍增求树上两点到LCA路径上的最小值即可。
#include<cstdio>
#include<cctype>
using namespace std;
#define MAXN 100010
#define INF 999999999
struct Edge{int to,next,w;}edge[MAXN*2];
int cnt,n,m,head[MAXN],deep[MAXN],fa[MAXN][21],w[MAXN][21];
bool vis[MAXN];
inline int min(int a,int b){return a<b?a:b;}
inline void swap(int &a,int &b){register int tmp=a;a=b;b=tmp;}
inline void read(int &a){
a=0;
register char ch=‘\0‘;register int f=1;
while(!isdigit(ch)&&ch!=‘-‘)ch=getchar();
if(ch==‘-‘)f=-f,ch=getchar();
for(;isdigit(ch);ch=getchar())a=a*10+ch-‘0‘;
a*=f;
}
inline void addedge(int from, int to, int w){
edge[++cnt].next=head[from];
edge[cnt].to=to;
edge[cnt].w=w;
head[from]=cnt;
}
inline void dfs(int node){
vis[node]=true;
for(int i=head[node]; i; i=edge[i].next){
int to=edge[i].to;
if(vis[to]) continue;
deep[to]=deep[node]+1;
fa[to][0]=node;
w[to][0]=edge[i].w;
dfs(to);
}
}
inline int lca(int x, int y)
{
int ans=INF;
if(deep[x]>deep[y]) swap(x,y);
for(int i=20; i>=0; i--)
if(deep[fa[y][i]]>=deep[x])
{
ans=min(ans, w[y][i]);
y=fa[y][i];
}
if(x==y) return ans;
for(int i=20; i>=0; i--)
if(fa[x][i]!=fa[y][i])
{
ans=min(ans, min(w[x][i], w[y][i]));
x=fa[x][i];
y=fa[y][i];
}
ans=min(ans, min(w[x][0], w[y][0]));
return ans;
}
int main()
{
#ifndef LOCAL
freopen("goods.in","r",stdin);
freopen("goods.out","w",stdout);
#endif
int x,y,z;
read(n);read(m);
for(int i=1; i<=n-1; i++)
{
read(x);read(y);read(z);
addedge(x,y,z);addedge(y,x,z);
}
for(int i=1; i<=n; i++)
if(!vis[i])
{
deep[i]=1;
dfs(i);
fa[i][0]=i;
w[i][0]=INF;
}
for(int i=1; i<=20; i++)
for(int j=1; j<=n; j++)
{
fa[j][i]=fa[fa[j][i-1]][i-1];
w[j][i]=min(w[j][i-1], w[fa[j][i-1]][i-1]);
}
for(int i=1; i<=m; i++)
{
read(x);read(y);
printf("%d\n",lca(x,y));
}
fclose(stdin);
fclose(stdout);
return 0;
}
Problem 3 数三角形(triangle.cpp/c/pas)
【题目描述】
给定一个 n×m 的网格,请计算三点都在格点上的三角形共有多少个。下图
为 4×4 的网格上的一个三角形。
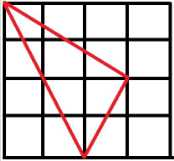
注意 :
三角形的三点不能共线。
m n×m 的网格 共有( ( n+1) ) ×( ( m+1) ) 个格点
【输入格式】
输入文件 triangle.in
输入一行,包含两个正整数 m,n。
【输出格式】
输出文件 triangle.out
输出一个正整数,为所求三角形数量。
【样例输入】
2 2
【样例输出】
76
【数据范围】
对于 30%的数据 n,m<=10
对于 60%的数据 n,m<=40
对于 100%的数据 n,m<=1000
solution: 计算一条线段的斜率,明显的,若三点共线则一定构不成三角形。枚举一条线段的两个端点之差即可计算出斜率。计算出全集,然后减掉不能构成三角形的方案数即可。
#include<cstdio>
using namespace std;
typedef unsigned long long ull;
ull m,n;
ull ans;
ull gcd(ull a,ull b){return !b?a:gcd(b,a%b);}
int main()
{
#ifndef LOCAL
freopen("triangle.in","r",stdin);
freopen("triangle.out","w",stdout);
#endif
scanf("%llu%llu",&m,&n);
m++;n++;
ans=m*n;
ans=ans*(ans-1)/2*(ans-2)/3;
for (ull a=0;a<=n;a++)
for (ull b=0;b<=m;b++)
if (a||b)
{
ull t=(gcd(a,b)-1)*(n-a)*(m-b);
if (!a||!b) ans-=t;
else ans-=2*t;
}
printf("%llu\n",ans);
fclose(stdin);
fclose(stdout);
return 0;
}
