评分卡系列（四）：泛化误差估计与模型调参

作者：JSong，时间：2017.10.21

本文大量引用了 jasonfreak ( http://www.cnblogs.com/jasonfreak ) 的系列文章，在此进行注明和感谢.

广义的偏差（bias）描述的是预测值和真实值之间的差异，方差（variance）描述距的是预测值作为随机变量的离散程度。《Understanding the Bias-Variance Tradeoff》当中有一副图形象地向我们展示了偏差和方差的关系：

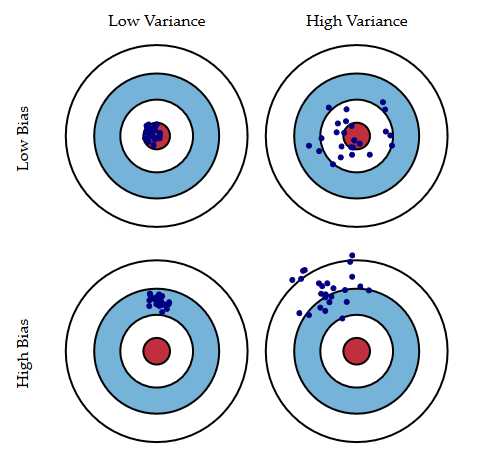
一、Bias-variance 分解

我们知道算法在不同训练集上学到的结果很可能不同，即便这些训练集来自于同一分布。对测试样本 x ,令 y_D 为 x 在数据集中的标记，y 为 x 的真实标记， f(x;D) 为训练集 D 上学的模型 f 在 x 上的预测输出。

在回归任务中，学习算法的期望输出为：

\[\bar{f}(x)=\mathbb{E}_{D}[f(x;D)]\]

使用样本数相同的不同训练集产生的方差为：

\[var(x)=\mathbb{E}_{D}[(f(x;D)-\bar{f}(x))^2]\]

噪声为

\[\varepsilon^2=\mathbb{E}_{D}[(y_{D}-y)^2]\]

我们将期望输出与真实标记之间的差别称为偏差（bias）：

\[bias^2(x)=(\bar{f}(x)-y)^2\]

为便于讨论，假定噪声期望为零，即

\[\mathbb{E}_D[y_D-y]=0\]

通过简单的多项式展开合并，对算法的期望泛化误差进行分解：

\[\begin{align} E(f;D)=&\mathbb{E}_{D}\left[(f(x;D)-y_D)^2\right]\=&\mathbb{E}_{D}\left[(f(x;D)-\bar{f}(x)+\bar{f}(x)-y_D)^2\right]\=&\mathbb{E}_{D}\left[(f(x;D)-\bar{f}(x))^2\right]+(\bar{f}(x)-y)^2+\mathbb{E}_{D}[(y_D-y)^2] \end{align}\]

于是有

\[E(f;D)=bias^2(x)+var(x)+\varepsilon^2\]

也就是说，泛化误差可分解为偏差、方差与噪声之和。

偏差和方差是有冲突的，下面是一个示意图。在训练不足（模型复杂度低）时，偏差主导了泛化误差率；随着训练程度的加深，方差逐渐主导了泛化误差率。

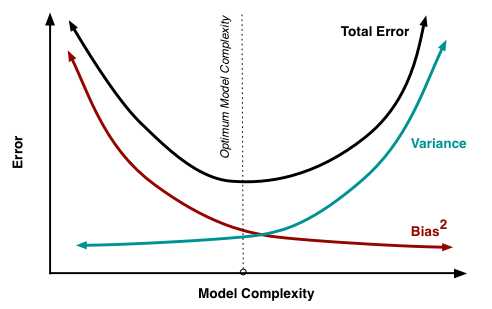
二、集成学习框架下的泛化误差分解

这一节内容节选自博客：《使用sklearn进行集成学习——理论》 (www.cnblogs.com/jasonfreak/p/5657196.html)

在bagging和boosting框架中，通过计算基模型的期望和方差，我们可以得到模型整体的期望和方差。为了简化模型，我们假设基模型的权重、方差及两两间的相关系数相等。由于bagging和boosting的基模型都是线性组成的，那么有：

\[E(f)=E(\sum_{i=1}^{m}\gamma_{i}\cdot_{}f_{i})=\sum_{i=1}^{m}\gamma_{i}\cdot_{}E(f_i)=\gamma\cdot\sum_{i}^{m}E(f_i)\]

和

\[\begin{align} Var(f)=&Var(\sum_{i}^{m}\gamma_{i}\cdot_{}f_{i})=Cov(\sum_{i}^{m}\gamma_{i}\cdot_{}f_{i},\sum_{i}^{m}\gamma_{i}\cdot_{}f_{i})\=&\sum_{i}^{m}\gamma_{i}^2\cdot_{}Var(f_i)+\sum_{i}^{m}\sum_{j\neq_{}i}^{m}2\rho\gamma_{i}\gamma_{j}\sqrt{Var(f_i)}\sqrt{Var(f_j)}\=&m^2\gamma^2\sigma^2\rho+m\gamma^2\sigma^2(1-\rho) \end{align}\]

2.1 bagging 的偏差和方差

对于bagging来说，每个基模型的权重等于 1/m 且期望近似相等（子训练集都是从原训练集中进行子抽样），故我们可以进一步化简得到：

\[E(f)=\gamma\cdot\sum_{i}^{m}E(f_i)=\frac{1}{m}m\mu=\mu\]

和

\[\begin{align} Var(F)=&m^2\gamma^2\sigma^2\rho+m\gamma^2\sigma^2(1-\rho)\=&m^2\frac{1}{m^2}\sigma^2\rho+m\frac{1}{m^2}\sigma^2(1-\rho)\=&\sigma^2\rho+\frac{\sigma^2(1-\rho)}{m} \end{align}\]

根据上式我们可以看到，整体模型的期望近似于基模型的期望，这也就意味着整体模型的偏差和基模型的偏差近似。同时，整体模型的方差小于等于基模型的方差（当相关性为1时取等号），随着基模型数（m）的增多，整体模型的方差减少，从而防止过拟合的能力增强，模型的准确度得到提高。但是，模型的准确度一定会无限逼近于1吗？并不一定，当基模型数增加到一定程度时，方差公式第二项的改变对整体方差的作用很小，防止过拟合的能力达到极限，这便是准确度的极限了。另外，在此我们还知道了为什么bagging中的基模型一定要为强模型，否则就会导致整体模型的偏差度低，即准确度低。

　　Random Forest是典型的基于bagging框架的模型，其在bagging的基础上，进一步降低了模型的方差。Random Fores中基模型是树模型，在树的内部节点分裂过程中，不再是将所有特征，而是随机抽样一部分特征纳入分裂的候选项。这样一来，基模型之间的相关性降低，从而在方差公式中，第一项显著减少，第二项稍微增加，整体方差仍是减少。

2.2 boosting 的偏差和方差

对于boosting来说，基模型的训练集抽样是强相关的，那么模型的相关系数近似等于1，故我们也可以针对boosting化简公式为：

\[E(f)=\gamma\sum_{i}^{m}E(f_i)\]

和

\[Var(F)=m^2\gamma^2\sigma^2\rho+m\gamma^2\sigma^2(1-\rho)=m^2\gamma^2\sigma^2\]

通过观察整体方差的表达式，我们容易发现，若基模型不是弱模型，其方差相对较大，这将导致整体模型的方差很大，即无法达到防止过拟合的效果。因此，boosting框架中的基模型必须为弱模型。

因为基模型为弱模型，导致了每个基模型的准确度都不是很高（因为其在训练集上的准确度不高）。随着基模型数的增多，整体模型的期望值增加，更接近真实值，因此，整体模型的准确度提高。但是准确度一定会无限逼近于1吗？仍然并不一定，因为训练过程中准确度的提高的主要功臣是整体模型在训练集上的准确度提高，而随着训练的进行，整体模型的方差变大，导致防止过拟合的能力变弱，最终导致了准确度反而有所下降。

基于boosting框架的 Gradient Tree Boosting 模型中基模型也为树模型，同 Random Forrest，我们也可以对特征进行随机抽样来使基模型间的相关性降低，从而达到减少方差的效果。

三、常见分类模型及其参数介绍

本文介绍的都是 scikit-learn 中的模型。

3.1 逻辑回归模型

在scikit-learn中，与逻辑回归有关的主要是这3个类。

• logisticRegression
• LogisticRegressionCV
• logistic_regression_path

其中LogisticRegression和LogisticRegressionCV的主要区别是LogisticRegressionCV使用了交叉验证来选择正则化系数C。而LogisticRegression需要自己每次指定一个正则化系数。另外logistic_regression_path类则比较特殊，它拟合数据后，不能直接来做预测，只能为拟合数据选择合适逻辑回归的系数和正则化系数，主要是用在模型选择的时候，一般情况用不到这个类，所以后面不再讲述logistic_regression_path类。

LogisticRegression 的参数使用如下：

class sklearn.linear_model.LogisticRegression(penalty=‘l2‘, dual=False, tol=0.0001, C=1.0, fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=‘liblinear‘, max_iter=100, multi_class=‘ovr‘, verbose=0, warm_start=False, n_jobs=1)

具体含义为：

3.2 集成学习模型

在scikit-learn中，与随机森林有关的有两个。

• RandomForestClassifier(): A random forest classifier.
• RandomForestRegressor(): A random forest regressor.

这里主要讲第一个，它的参数如下：

class sklearn.ensemble.RandomForestClassifier(n_estimators=10, criterion=’gini’, max_depth=None, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_features=’auto’, max_leaf_nodes=None, min_impurity_decrease=0.0, min_impurity_split=None, bootstrap=True, oob_score=False, n_jobs=1, random_state=None, verbose=0, warm_start=False, class_weight=None)

与GBDT有关的也是两个。

• GradientBoostingClassifier([loss, …])： Gradient Boosting for classification.
• GradientBoostingRegressor([loss, …])： Gradient Boosting for regression.

其中分类模型的参数如下：

class sklearn.ensemble.GradientBoostingClassifier(loss=’deviance’, learning_rate=0.1, n_estimators=100, subsample=1.0, criterion=’friedman_mse’, min_samples_split=2, min_samples_leaf=1, min_weight_fraction_leaf=0.0, max_depth=3, min_impurity_decrease=0.0, min_impurity_split=None, init=None, random_state=None, max_features=None, verbose=0, max_leaf_nodes=None, warm_start=False, presort=’auto’)

这两个模型的参数介绍如下：

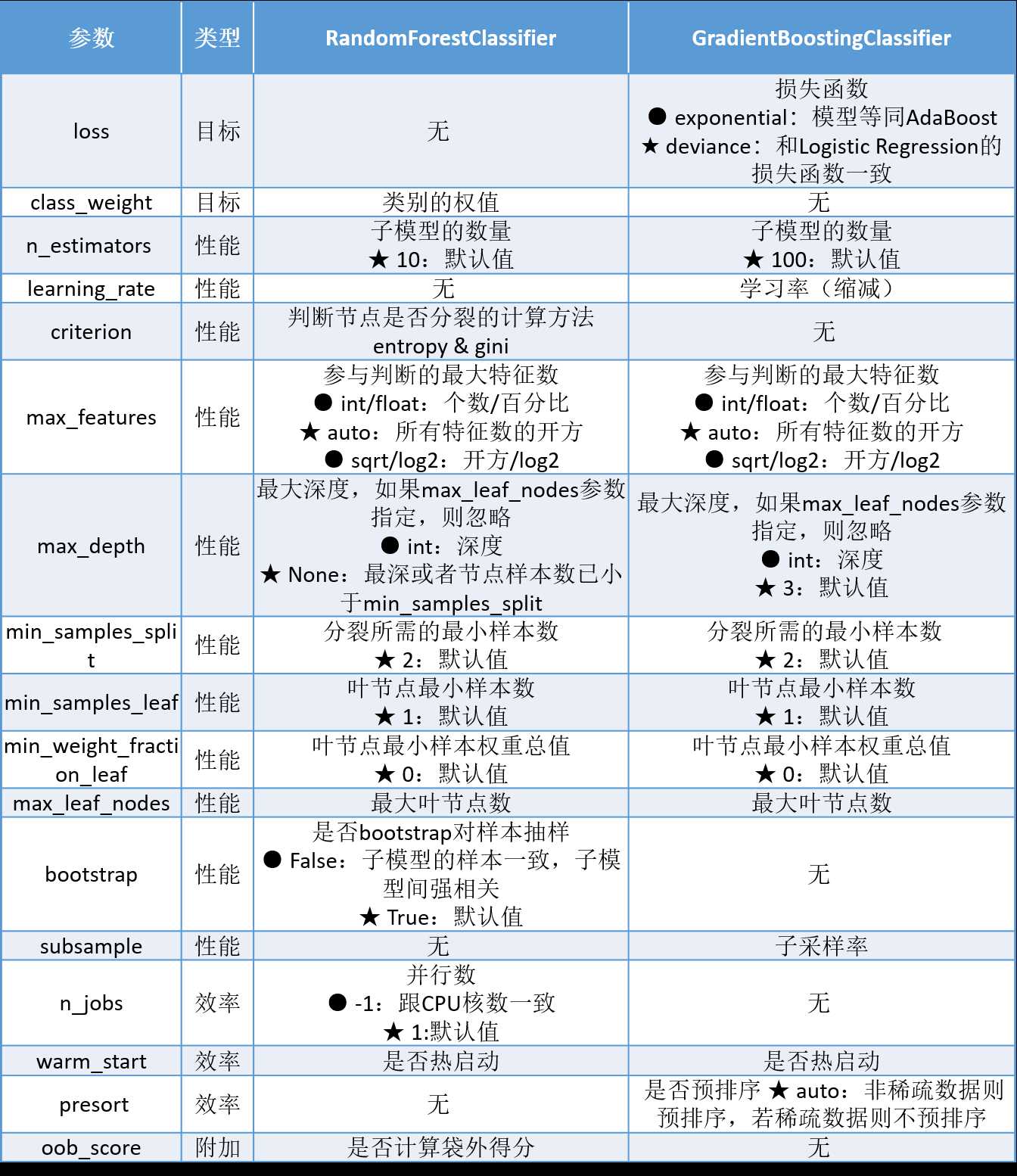
在上一节我们对bagging和boosting两种集成学习技术的泛化误差估计有了初步的了解。Random Forest的子模型都拥有较低的偏差，整体模型的训练过程旨在降低方差，故其需要较少的子模型（n_estimators默认值为10）且子模型不为弱模型（max_depth的默认值为None），同时，降低子模型间的相关度可以起到减少整体模型的方差的效果（max_features的默认值为auto）。

另一方面，Gradient Tree Boosting的子模型都拥有较低的方差，整体模型的训练过程旨在降低偏差，故其需要较多的子模型（n_estimators默认值为100）且子模型为弱模型（max_depth的默认值为3），但是降低子模型间的相关度不能显著减少整体模型的方差（max_features的默认值为None）。

四、分类模型的调参方法

调参是一个最优化问题。如果样本量不是非常大，计算资源也足够，那我们可以直接用网格搜索进行穷举。例如在随机森林算法中，可以用sklearn提供的GridSearchCV函数来调参。

param_test1 ={‘n_estimators‘:range(10,71,10)，‘max_features‘:range(20,50,1)}  
gsearch1= GridSearchCV(estimator =RandomForestClassifier(min_samples_split=100,  
                                 min_samples_leaf=20,max_depth=8,random_state=10),   
                       param_grid =param_test1,scoring=‘roc_auc‘,cv=5)  
gsearch1.fit(X,y)  
gsearch1.grid_scores_, gsearch1.best_params_, gsearch1.best_score_

对于小数据集，我们还能这么任性，但是参数组合爆炸，在大数据集上，如果用网格搜索，那真的要下一个猴年马月才能看到结果了。而且实际上网格搜索也不一定能得到全局最优解，而另一些研究者从解优化问题的角度尝试解决调参问题。

坐标下降法是一类非梯度优化算法。算法在每次迭代中，在当前点处沿一个坐标方向进行一维搜索以求得一个函数的局部极小值。在整个过程中循环使用不同的坐标方向。对于不可拆分的函数而言，算法可能无法在较小的迭代步数中求得最优解。为了加速收敛，可以采用一个适当的坐标系，例如通过主成分分析获得一个坐标间尽可能不相互关联的新坐标系（如自适应坐标下降法）。

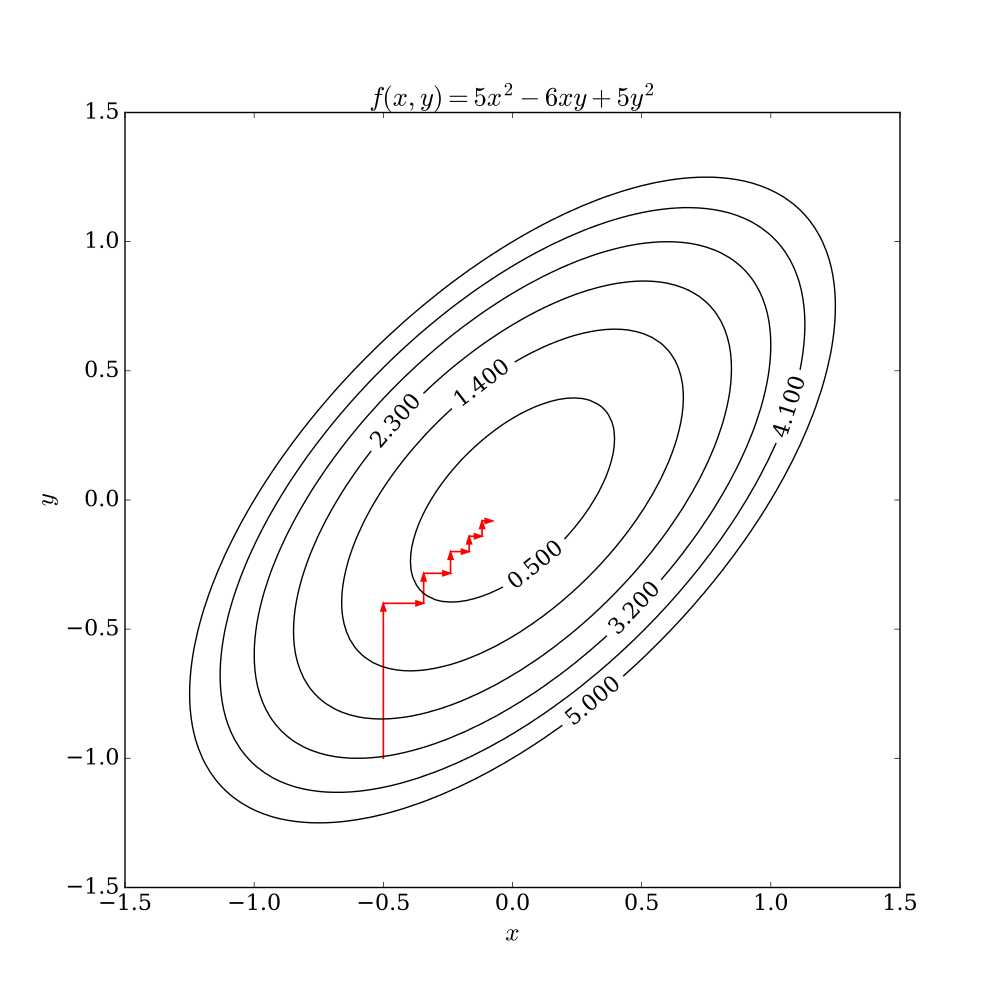
我们最容易想到一种特别朴实的类似于坐标下降法的方法，与坐标下降法不同的是，其不是循环使用各个参数进行调整，而是贪心地选取了对整体模型性能影响最大的参数。参数对整体模型性能的影响力是动态变化的，故每一轮坐标选取的过程中，这种方法在对每个坐标的下降方向进行一次直线搜索（line search）。首先，找到那些能够提升整体模型性能的参数，其次确保提升是单调或近似单调的。这意味着，我们筛选出来的参数是对整体模型性能有正影响的，且这种影响不是偶然性的，要知道，训练过程的随机性也会导致整体模型性能的细微区别，而这种区别是不具有单调性的。最后，在这些筛选出来的参数中，选取影响最大的参数进行调整即可。

另外无法对整体模型性能进行量化，也就谈不上去比较参数影响整体模型性能的程度。我们还没有一个准确的方法来量化整体模型性能，只能通过交叉验证来近似计算整体模型性能。然而交叉验证也存在随机性，假设我们以验证集上的平均准确度作为整体模型的准确度，我们还得关心在各个验证集上准确度的变异系数，如果变异系数过大，则平均值作为整体模型的准确度也是不合适的。

五、评分卡实践

参考文献

[1]. Understanding the Bias-Variance Tradeoff

[2]. 使用sklearn进行集成学习——理论

http://scikit-learn.org/stable/modules/model_evaluation.html

http://blog.csdn.net/u012969412/article/details/72973055

[使用sklearn进行集成学习——实践] ( www.cnblogs.com/jasonfreak/p/5720137.html )