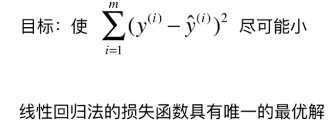梯度下降法
- 不是一个机器学习算法
- 是一种基于搜索的最优化方法
- 作用：最小化一个损失函数
- 梯度上升法：最大化一个效用函数
举个栗子
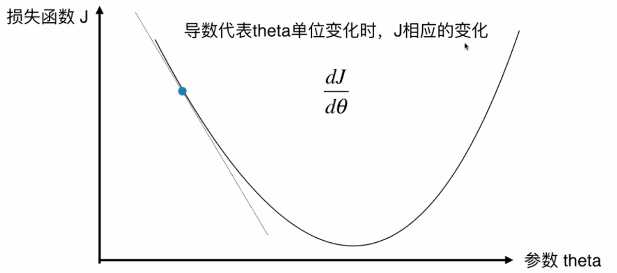
直线方程：导数代表斜率
曲线方程：导数代表切线斜率
导数可以代表方向，对应J增大的方向。对于蓝点，斜率为负，西塔减少时J增加，西塔增加时J减少，我们想让J减小，对应导数的负方向，因此前面需要加上负号。
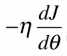（伊塔对应步长）-------（1）
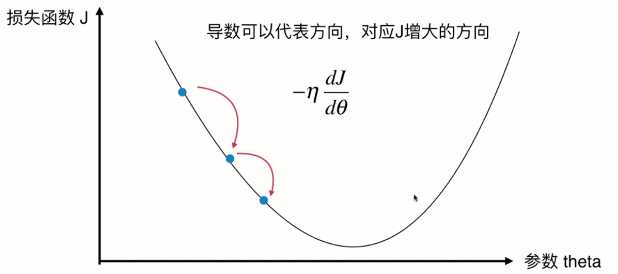
用当前点的西塔加上（1）式，得到新的西塔。因为导数是负值，前面又有负号，所以整个是正值，加上一个正值对应西塔在增大。
多维函数中，对各维求导数，其实就是梯度。
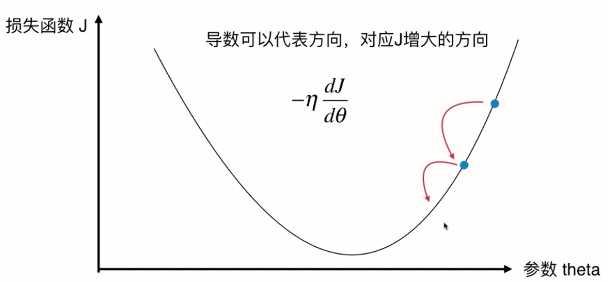
当点取在右边时，（1）式也成立。此时斜率为正，西塔增加J增加，西塔减少J减少，我们想让J减少因此我们前面也要加上负号。此时相当于 西塔减去一个正值 -> 西塔变小了 -> 在向着左边移动。
我们可以想成这是一个山谷，放一个球下来，球自然会滚到最低处。梯度下降即在模拟这个过程。球滚落的速率 即由 伊塔 决定。
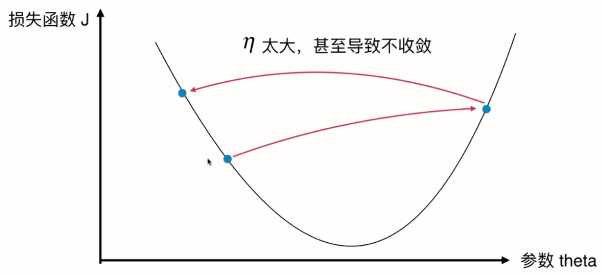
并不是所有函数都有唯一的极值点
如果从最右侧的点开始搜索，找到局部最优解后就结束了。
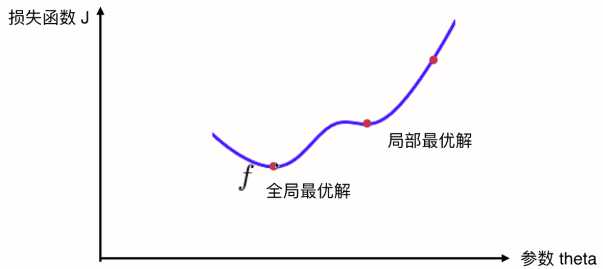
注：对于线性回归来说，
