对红黑树的操作在最坏的情形下花费O(logN)时间,相对AVL树来说,性质比较多但是换取了插入和删除时少量的旋转操作。
因为书中说的不清楚,特查看wiki做本文笔记~~
性质
- 节点是红色或者黑色
- 根为黑色的
- 所有叶子为黑色
- 每个红色节点必须有两个黑色的子节点
- 从任一节点到其每个叶子的所有简单路径都包含相同数目的黑色节点

操作
红黑树的只读操作和普通二叉查找树的操作是一样,但是插入和删除要考虑相邻节点的情况,来重新平衡性质
插入
下面用叔父节点来指代父节点的兄弟节点,当插入新节点的时候,可能会有下面几个情形需要进行修复
1.新节点N位于树的根上,没有父节点,这个时候把它重绘为黑色就可以
2.新节点父节点为黑色,新节点则为红色,满足性质
3.父节点P和叔父节点U都是红色,将两个重绘为黑色并重绘祖父节点为红色,如下
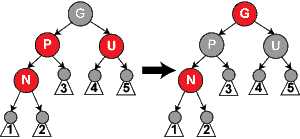
然后把G当做当前节点进行操作
4.父节点P是红色而叔父节点为黑色,P是G的左子节点,N是P的右子节点,也就是AVL的之字形(还有另一种对称情况)
这种情况下需要进行一次左旋转
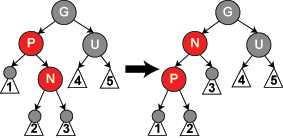
5.父节点P是红色,叔父节点是黑色,N是P的左子节点,P是G的左子节点,对G进行一次右旋转
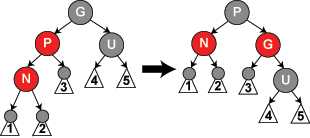
删除
要么在它的左子树中的最大元素、要么在它的右子树中的最小元素,并把它的值转移到要删除的节点中;接着就可以删除被复制值的节点。
它必定有少于两个非叶节点,所以问题可以简化为如何删除最多有一个儿子节点的问题!!!
先根据被删除节点来划分
- 红色节点,简单用黑色儿子替换它就可
- 黑色节点且儿子为红色,替换节点后,重绘节点为黑色
这样就剩下删除节点是黑色,而且儿子为黑色的情况了,假设已经替换好了儿子为N(原位置的已经删除),兄弟节点为S,P为父亲,SL、SR为S的左儿子右儿子
如果N和它原来的父亲都是黑色(父亲已经被删除),会导致通过N比不通过N少了一个黑色节点,需要分为下面几个情况解决
1.N是新的根,已经完成了
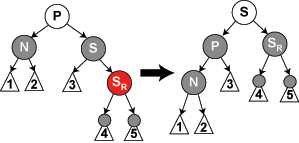
2.S为红色,对P做左旋转,S作为N的祖父,对调P和S的颜色,这样会转变为4、5、6
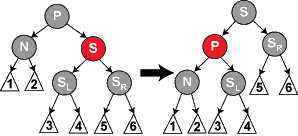
3.P、S、SL、SR都是黑色的,重绘S为红色
因为删除N的初始的父亲使通过N的所有路径少了一个黑色节点,这使事情都平衡了起来。但是,通过P的所有路径现在比不通过P的路径少了一个黑色节点,所以仍然违反性质5。要修正这个问题,我们要从情形1开始,在P上做重新平衡处理。
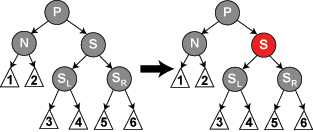
4.S、SL、SR都是黑色的,P是红色,交换S和P的颜色
这不影响不通过N的路径的黑色节点的数目,但是它在通过N的路径上对黑色节点数目增加了一,添补了在这些路径上删除的黑色节点。
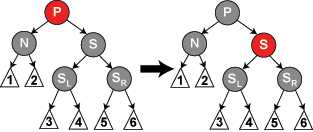
5.S 、SR是黑色,SL是红色,N是P的左儿子,对S做右旋转,交换S和新父亲的颜色,进入6
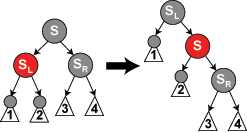
6.S是黑色,SR是红色,N是P的左儿子,对P做左旋转,交换N的父亲和S的颜色,使S的右儿子为黑色
此时,如果一个路径不通过N,则有两种可能性:
- 它通过N的新兄弟。那么它以前和现在都必定通过S和N的父亲,而它们只是交换了颜色。所以路径保持了同样数目的黑色节点。
- 它通过N的新叔父,S的右儿子。那么它以前通过S、S的父亲和S的右儿子,但是现在只通过S,它被假定为它以前的父亲的颜色,和S的右儿子,它被从红色改变为黑色。合成效果是这个路径通过了同样数目的黑色节点。