GBDT
序言
GBDT (Gradient Boosting Decision Tree)又叫MART (Multiple Additive Regression Tree),是一种迭代的决策树算法,即该算法由多棵决策树组成,所有决策树的预测结果累加起来做最终答案。
正文
Gradient Boosting基本思想
Gradient Boosting 基于“三个臭皮匠赛过诸葛亮”的思想。与前面随机森林Bagging的思想不同,我们下面举一个直观的金融相关的例子进行对比。
假设你现在希望较准确的对某个公司进行股票开盘价定价,但是你完全没有金融相关的知识,并且由于金融市场的千变万化,仅仅参考一个专业金融领域工作者的看法,那风险将会非常大。
考虑到这些原因,那么你可以通过Bagging或者Gradient Boosting的思想,集合众人的智慧帮你进行股票的定价。如果你通过搜集一群相似的人(专业金融领域工作者)对该公司股票的定价,并且你认为大家的水平一致,所以你简单计算这些定价的平均值作为最终的定价,那么就相当于你采用了Bagging的思想;另外,如果你邀请了个不同领域的人,他们可以没有太多专业的金融知识,比如普通的股民、一些中小企业的创业者、大企业的高管。你们集合在一个房间中,你先说了你认为可能的定价元/股,随后你邀请的这些人开始了发言:“我觉得这个高(低)了,至少也得减(加)n元/股”,然而你认为不能完全参考别人的发言,所以你参考后回答道:“参考了你的看法,我觉得定价可能是价元/股”,这里的是一个属于之间的数,表示了你对发言者的信任程度。当所有人发言完之后,你也确定了最后的定价,那么你就相当于采用了Gradient Boosting的思想。
Gradient Boosting的关键与特点
在上面的例子中,如果你仔细阅读你会发现,与Bagging相比,Gradient Boosting有两个非常关键的地方:①你可以邀请不专业的决策者,②你需要邀请不同领域的人。以及一个重要特点:你不需要完全信任每个人的定价。
这两个关键也代表了Gradient Boosting的关键性质:①基模型的预测能力可以非常弱(例如树深很小的决策树),②不同的基模型的关注点不同(例如GBDT每颗决策树关注于预测先前的决策树没能预测到的残差部分)。
而对每颗树学习到的残差部分的信任程度,实际上称为shrinkage(收缩量)或learning rate(学习率),很大程度的影响了GBDT的实际应用效果。如果你完全信任取,此时,每次新的定价都完全取决于最新发言者的定价,那么你股票的定价将会非常不稳定;而如果你取的非常小,那么最终的结果将非常大程度的取决于你最初的定价结果。
GBDT实例讲解
竟然我们学习了决策树,现在又形象的介绍了Gradient Boosting的思想,那么我们现在已经可以进入GBDT(Gradient Boosting Decision Tree)的实例讲解了。在实例讲解前,我们有必要看看DT(决策树)作为一个模型,到底是如何与GB(Gradient Boosting)结合起来的,其实非常简单,DT作为模型——“决策者”,不难想到,每颗决策树学习不同的残差——相当于拥有不同领域知识的决策参与者。下面我们用虚构的数据,介绍GBDT是如何实现公司上市价格定价的。
|
公司 名称 |
资产 增长率(%) |
所属 行业 |
实际 上市价格(元/股) |
|
公司A |
8 |
汽车制造 |
10 |
|
公司B |
18 |
汽车维修 |
12 |
|
公司C |
4 |
汽车维修 |
6 |
|
公司D |
12 |
汽车制造 |
16 |
(图一)
首先我们训练生成第一棵决策树,该决策树使用所属行业这个属性去拟合上市价格,如图一所示,由于公司A,公司D 同属于汽车制造,公司B,公司C同属于汽车维修,他们被分成两拨,每拨用平均上市价格作为预测值。此时的残差=实际值-预测值,所以A的残差为10-13=-3。以此类推,得到A,B,C,D的残差为-3,3,-3,3。
GBDT以计算得到的残差作为新的预测目标,以此训练得到第二棵决策树(图二),该决策树根据其资产增长率是否大于10%作为分割点,将A,C 与 B,D分成两拨,训练结束。
因此综合两棵树的学习结果:
预测A上市股价 = 13-3=10
预测B上市股价 = 9+3=12
预测C上市股价 = 9-3=6
预测D上市股价 = 13+3=16
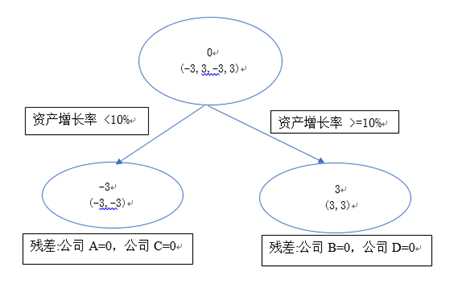
(图二)
总结
在本章中,我们通过一个股票开盘价定价的例子介绍了GBDT的思想,并巧妙的将GBDT的特点及关键部分也包含到这个例子中,随后,我们从特殊到一般,重新讲述了GBDT的特点及关键部分,这不难看出我们对其的重视,希望同学们能仔细体会这部分内容。
参考文献
https://www.jianshu.com/p/005a4e6ac775
