题目:Luogu 3437
这是今天 SLYZ 考试的一道题,一道二维线段树的入门题,惨的是我之前没有写过二维线段树,更不知道什么是标记用久化,于是自己 YY 出了标记永久化,但由于我十分的菜所以写炸了。
如果按照普通线段树的方法来做,发现外层的 x 树是无法 pushdown 和 maintain 的,怎么办?
如果遇到无法下传标记的情况,大概就要用到标记永久化了。
所谓标记永久化,就是不下传标记,查询时路过该节点,就加上这个节点的标记。
1. 如何省去 maintain 操作
用数组 val[ ] 来记录一个节点的值。
在 update 之前,先 query 出将要更新的节点的原值,设变量 value 为这个原值加上要加的值,然后 update。
update 时,沿路用 value 更新路过的节点,每到达一个节点,val[cur] = max(val[cur], value);
这就相当于 maintain 的时候用左右儿子节点更新当前节点。
2. 如何省去 pushdown 操作
用数组 tag[ ] 记录永久化的标记。
在 update 中,若到达了目标节点(Ql <= l && r <= Qr),需要用 value 更新当前节点的 tag,即 tag[cur] = max(tag[cur], value);
这一步有什么用呢?
在 query 的时候,若路过一个节点,需要将它的 tag 加入计算。如下图。
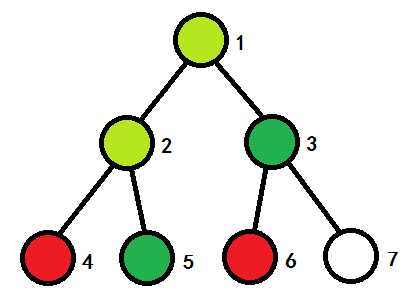
假如之前更新过 3 号和 5 号点,则 val[1]、val[2]、val[3]、val[5] 都有变动,并且 tag[1] 和 tag[3] 处有标记。
此时若要查询 4 号点和 6 号点的值:
查询 4 号点,由于 tag[1] 和 tag[2] 为空,所以答案为 val[4];
查询 6 号点,3 号点的标记按理说应该下传,但我们不下传,所以答案为 max(tag[3], val[6]);
详见代码。
1 #include <cstdio> 2 #include <string> 3 4 int read() { 5 int x = 0, f = 1; 6 char c = getchar(); 7 while (!isdigit(c)) { 8 if (c == ‘-‘) f = -1; 9 c = getchar(); 10 } 11 while (isdigit(c)) { 12 x = (x << 3) + (x << 1) + (c ^ 48); 13 c = getchar(); 14 } 15 return x * f; 16 } 17 18 int max(int x, int y) { 19 if (x >= y) return x; return y; 20 } 21 22 const int N = 4005; int D, S; 23 24 struct inNode { 25 int val[N], tag[N]; 26 void update(int cur, int l, int r, int y1, int y2, int value) { 27 val[cur] = max(val[cur], value); 28 if (y1 <= l && r <= y2) { 29 tag[cur] = max(tag[cur], value); 30 } else { 31 int mid = l + ((r - l) >> 1); 32 if (y1 <= mid) update(cur << 1, l, mid, y1, y2, value); 33 if (mid < y2) update(cur << 1 | 1, mid + 1, r, y1, y2, value); 34 } 35 } 36 37 int query(int cur, int l, int r, int y1, int y2) { 38 if (y1 <= l && r <= y2) return val[cur]; 39 int mid = l + ((r - l) >> 1), res = tag[cur]; 40 if (y1 <= mid) res = max(res, query(cur << 1, l, mid, y1, y2)); 41 if (mid < y2) res = max(res, query(cur << 1 | 1, mid + 1, r, y1, y2)); 42 return res; 43 } 44 }; 45 46 struct outNode { 47 inNode val[N], tag[N]; 48 void update(int cur, int l, int r, int x1, int x2, int y1, int y2, int value) { 49 val[cur].update(1, 1, S, y1, y2, value); 50 if (x1 <= l && r <= x2) { 51 tag[cur].update(1, 1, S, y1, y2, value); 52 } else { 53 int mid = l + ((r - l) >> 1); 54 if (x1 <= mid) update(cur << 1, l, mid, x1, x2, y1, y2, value); 55 if (mid < x2) update(cur << 1 | 1, mid + 1, r, x1, x2, y1, y2, value); 56 } 57 } 58 59 int query(int cur, int l, int r, int x1, int x2, int y1, int y2) { 60 if (x1 <= l && r <= x2) return val[cur].query(1, 1, S, y1, y2); 61 int mid = l + ((r - l) >> 1), res = tag[cur].query(1, 1, S, y1, y2); 62 if (x1 <= mid) res = max(res, query(cur << 1, l, mid, x1, x2, y1, y2)); 63 if (mid < x2) res = max(res, query(cur << 1 | 1, mid + 1, r, x1, x2, y1, y2)); 64 return res; 65 } 66 } tree; 67 68 int main() { 69 D = read(), S = read(); int n = read(); ++ D, ++ S; 70 for (int i = 1; i <= n; ++ i) { 71 int d = read(), s = read(), w = read(), 72 x = read(), y = read(); ++ x, ++ y; 73 int tmp = tree.query(1, 1, D, x, x + d - 1, y, y + s - 1); 74 tree.update(1, 1, D, x, x + d - 1, y, y + s - 1, tmp + w); 75 } 76 printf("%d\n", tree.query(1, 1, D, 1, D, 1, S)); 77 return 0; 78 }
