1序言
要明白什么是SVM,便得从分类说起。本书开头已经提到,分类作为数据挖掘领域中一项非常重要的任务,它的目的是学会一个分类函数或分类模型(或者叫做分类器),而支持向量机本身便是一种监督式学习的方法, 它广泛的应用于统计分类以及回归分析中。
支持向量机SVM是一种比较抽象的算法概念,全称是 Support Vector Machine ,它通过寻求结构化风险最小来提高学习机泛化能力,实现经验风险和置信范围的最小化,从而达到在统计样本量较少的情况下,亦能获得良好统计规律的目的。
2 什么是支持向量机
在介绍支持向量机之前,首先复习一下超平面的概念:在几何中,n维空间V的超平面是尺寸为n-1的子空间,例如平面中的直线、三维空间中的平面,以此类推,在多维空间下,如果用一个超平面就把数据分为了两类。这个超平面我们叫它为分离超平面。哪个是我们最终要选择的呢?让我们看一个例子:
下表是某金融公司调研的到的一些基金数据节选,表中有风险程度,年回报率和基金评价三部分
|
风险程度 |
年回报率 |
基金评价 |
风险程度 |
年回报率 |
基金评价 |
|
0.62 |
3.2% |
差 |
0.39 |
8.4% |
优 |
|
0.74 |
3.8% |
差 |
0.42 |
9.2% |
优 |
|
0.81 |
3.6% |
差 |
0.23 |
10.4% |
优 |
|
0.65 |
6.2% |
差 |
0.44 |
5.4% |
优 |
|
0.96 |
2.4% |
差 |
0.20 |
6.1% |
优 |
以风险为横轴,回报率为纵轴绘制散点图,红点代表低风险高回报的优质基金,蓝色点为不良基金:
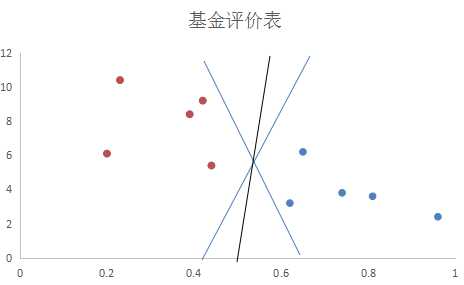
上图中,对于目前的基金数据,蓝色和黑色的直线(在二维特征空间,分离超平面为直线)都可以很可以很好的进行分类。但是,通过已知数据建立分离超平面的目的,是为了对于未知数据进行分类的。如果我们现在再加入四条基金数据
|
风险程度 |
年回报率 |
风险程度 |
年回报率 |
|
0.46 |
3.2% |
0.50 |
8.2% |
|
0.58 |
7.3% |
0.62 |
2.3% |
在下图中,绿色的圆点图案就是新加入的真实数据。
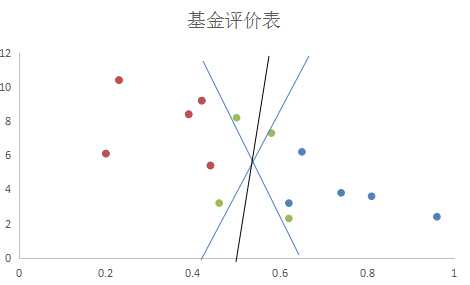
这时候我们就可以看出不同的分离超平面的选择对于分类效果的影响了。有的蓝线会将三个点都划归蓝色圆圈,有的绿点则直接落在了蓝线上,那么蓝线和黑线留下谁?我们认为,已有的训练数据中,每个元素距离分离超平面都有一个距离。在添加超平面的时候,尽可能的使最靠近分离超平面的那个元素与超平面的距离变大。这样,加入新的数据的时候,分得准的概率会最大化。感知器模型和逻辑回归都不能很好的完成这个工作,该我们的支持向量机(support vector machine,SVM)出场了。
首先,SVM将函数间隔(|WTX+b|,将特征值代入分离超平面的方程中,得到的绝对值)归一化,归一化的目的是除掉取值尺度的影响;其次,对所有元素求到超平面的距离,(这个距离是,也就是几何间隔)。给定一个超平面P,所有样本距离超平面P的距离可以记为,这其中最小的距离记为Dp,SVM的作用就是找到Dp最大的超平面。
如上图所示,黑线最好地将加入的新基金数据进行了划分,因此明显优于其他两条。
可以看出,大部分数据对于分离超平面都没有作用,能决定分离超平面的,只是已知的训练数据中很小的一部分。这与逻辑回归有非常大的区别。上图中,决定黑色的这条最优分离超平面的数据只有上方的一个红色的数据点和下方的两个蓝色的数据点。这些对于分离超平面有着非常强大影响的数据点也被称为支持向量。
3 黑科技-核函数
现实往往是很残酷的,一般的数据是线性不可分的,也就是找不到一条线将两种点很好的分类,例如:我们现在希望通过基金的风险程度来评价基金,显然,如果基金风险过高,投资者随时面临亏本的风险,但如果风险率极低,那意味着这只基金有可能资产配置过于保守,盈利肯定也不可观,因此,我们不妨假设当基金的某风险系数x在(0,1)之间时将这支基金评价为优,当风险系数小于0或大于1时则评价为差。公式如下:
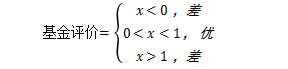
但此时问题出现了,我们无法在1维空间中找到分离超平面(一维空间中的分离超平面是一个点)。
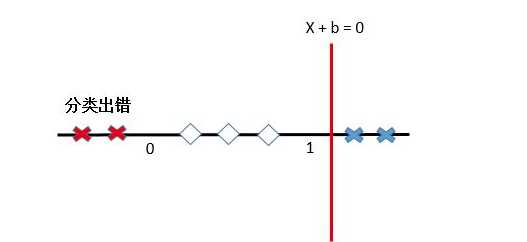
这就要说到SVM的黑科技—核函数技巧。核函数可以将原始特征映射到一个高维特征空间中,解决原始空间的线性不可分问题。继续刚才那个数轴:

如果我们将原始的一维特征空间映射到二维特征空间x2和x,那么就可以找到分离超平面x2-x=0。当x2-x<0的时候,就可以判别为类别1,当x2-x>0的时候,就可以判别为类别0。如下图:
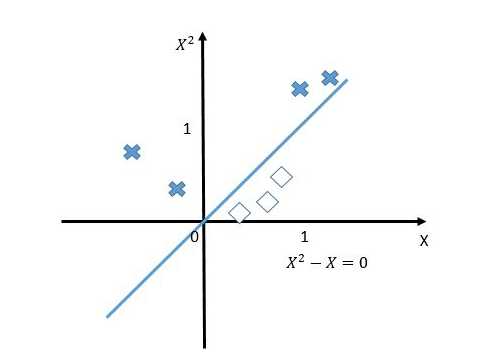
再将x2-x=0映射回原始的特征空间,就可以知道在0和1之间的实例类别是1,剩下空间上(小于0和大于1)的实例类别都是0。
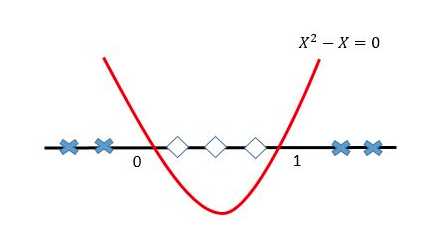
利用特征映射,就可以将低维空间中的线性不可分问题解决了,这就是特征映射的神奇之处了。核函数除了能够完成特征映射,而且还能把特征映射之后的内积结果直接返回,大幅度降低了简化了工作,这也是采用核函数的原因。
4 异常值的处理-松弛变量的引入
在原始空间线性不可分时,可以映射到高维空间之后,转换为线性可分的问题。但是万一映射之后还是不能线性可分,该如何处理呢?再比如正常的数据中混入了异常数据:
|
风险程度 |
年回报率 |
基金评价 |
|
0.51 |
8.6% |
差 |
异常数据很有可能会使应该的最佳分离超平面移位,或者直接使数据变得线性不可分。又怎么办?
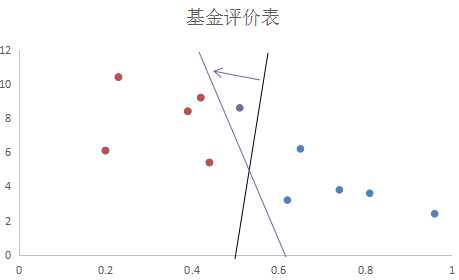
上图中用紫色的圆圈就是一个异常值,这个异常值的存在,使得分离超平面发生了移位。这时候就该引入松弛变量了。松弛变量可以允许某些数据点在不满足分离超平面两边的类别要求,从而使得某些严格线性不可分的数据集也可以使用SVM进行分类了。如下图的虚线所示,紫色圆圈代表的异常数据正好在允许的范围内,分离超平面没有受到影响而改变。
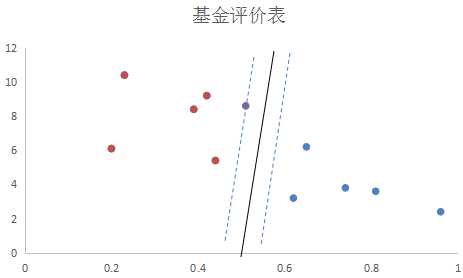
最后让我们总结一下,SVM解决问题的方法描述起来大概有以下几步:
(1)把所有的样本和其对应的分类标记交给算法进行训练。
(2)如果发现线性可分,那就直接找出超平面。
(3)如果发现线性不可分,那就映射到高一维维空间,找出超平面。
(4)如果仍然不可分,引入松弛变量。
(5)最后得到超平面的表达式, 也就是分类函数。
总之,SVM的基本思想就是求解能够正确划分数据集并且几何间隔最大的分离超平面。通俗讲就是样本点到分离超平面的最小间隔的最大化,即对最难分的样本点(离超平面最近的点)也有足够大的确信度将它们分开。
参考文献:
1 知乎专栏《白话SVM》 https://zhuanlan.zhihu.com/p/21301974
2 CSDN博客《SVM》 http://blog.csdn.net/xuelabizp/article/details/51122514
