题目背景
在一个渺远的海洋中,一场世纪大战级别的游戏上演了。
感谢 lsq 本人参与验题
题目描述
这块海洋上有n个小岛,小岛有m座石桥相连。有一些小岛上有wzt埋下的奖赏,它们非常诱人。它们的诱惑力用整数ki描述。而一些小岛上有lsq的雇佣兵,他们有一个价格,用整数bi描述。lsq必须花钱,他的雇佣兵才会帮他寻找奖赏。
雇佣兵的价格并不会变。对于每一个雇佣兵,在寻找过程中,他会越过一座座的桥,这过程中,他的价格会 加上他所经过的所有桥的长度 。
遗憾的是,不只有桥的阻挡,每座岛上有许多猛兽,虽然雇佣兵们都英勇无比,但驱逐猛兽的过程会让人很不爽。因此,对于每一个雇佣兵,价格会 加上他所经过的所有岛(包括出发岛)上的猛兽数量之和。
lsq了解这里的一切情况,他需要做出决策,即决定他的每个雇佣兵应该去找哪个奖赏。lsq的目的是找到所有奖赏,并取得最大收益。每个雇佣兵只能雇佣一次。
收益的定义为: 所有奖赏的诱惑力减去lsq花的所有的钱
lsq的决策异常艰难,于是只好请 AK过NOI 的你来帮忙。
输入输出格式
输入格式:
第一行4个数,n(小岛总数),m(桥总数),a(lsq的雇佣兵总人数),b(奖赏总数)
接下来一行n个数,表示每个小岛上的猛兽数量
接下来m行,每行三个数u,v,w,表示u号小岛与v号小岛之间有一座长度为w的桥相连
接下来a行,每行两个数qi,pi,表示i号雇佣兵价格为qi,初始位置为pi号小岛
接下来b行,每行两个数ki,qi,表示i号奖赏的诱惑力为ki,位置为qi号小岛
输出格式:
如果能找到所有奖赏,输出“Yes”,并在下一行输出能达到的最大满意度。
如果不能找到所有奖赏,输出“No”,并在下一行输出最多能找到多少奖赏。
输入输出样例
说明
对于30% 的数据,满足n<=200,m<=200,b<=a<=30
对于50% 的数据,满足n<=500,m<=800,b<=a<=100
对于100% 的数据,满足n<=1000,m<=15000,b<=a<=300,其余数据保证不会爆int(Pascal语言为longint)
 \
\
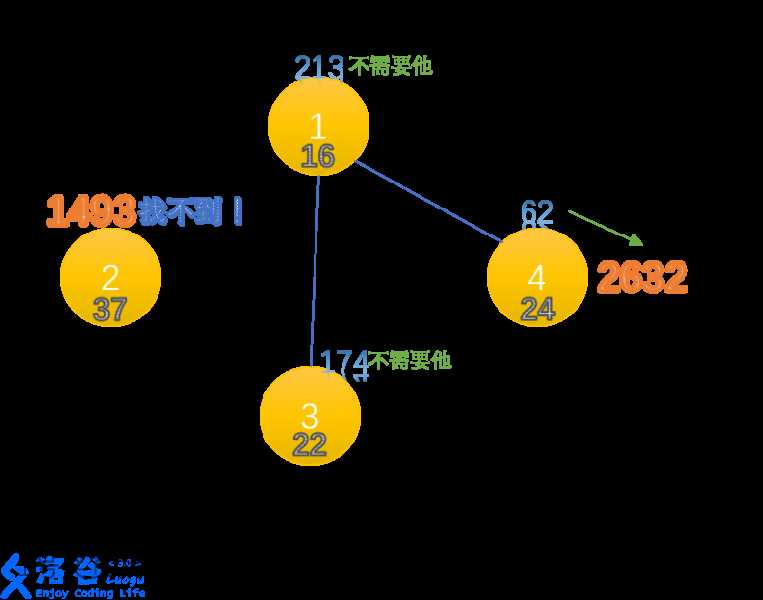
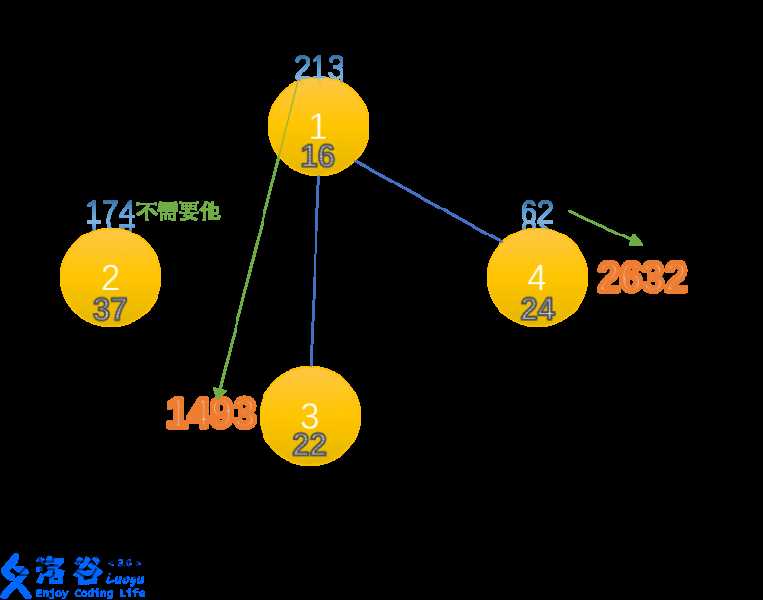
正解:最小费用最大流。
租每一个雇佣兵,我们就从超级源向这个雇佣兵所在岛屿连一条容量为1(因为只能雇佣一次),费用为该雇佣兵价格的边。
对于每座桥,我们看作是一条连接点的无向边。则从该桥两边向彼此连一条容量为INF,费用为该桥长度的边。
对于每座岛上的野兽,我们可以拆点。把该岛拆成入点和出点,入点向出点连一条容量为INF,费用为该岛野兽数量的边。
对于每一个奖赏,都向超级汇连一条长度为1(因为只能取一次),费用为0的边。
最后求解最小费用最大流即可。
若最大流流量小于宝藏数量,则无法获得所有的奖赏。输出最大流的流量。
否则可以获得所有的宝藏。输出所有奖赏的诱惑力减去最小费用。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<queue> 6 #include<cstring> 7 #include<string> 8 #define ll long long 9 #define DB double 10 #define inf 2000000000 11 using namespace std; 12 inline int read() 13 { 14 int x=0,w=1;char ch=getchar(); 15 while(!isdigit(ch)){if(ch==‘-‘) w=-1;ch=getchar();} 16 while(isdigit(ch)) x=(x<<3)+(x<<1)+ch-‘0‘,ch=getchar(); 17 return x*w; 18 } 19 const int N=1000010; 20 struct node{ 21 int u,v,c,fl,ne; 22 }e[N]; 23 int h[N],tot,n,m; 24 int a,b,sum; 25 int d[N],v[N],S,T; 26 queue<int>q; 27 void add1(int u,int v,int c,int fl) 28 { 29 tot++;e[tot]=(node){u,v,c,fl,h[u]};h[u]=tot; 30 } 31 void add(int u,int v,int c,int fl) 32 { 33 add1(u,v,c,fl);add1(v,u,-c,0); 34 } 35 bool bfs() 36 { 37 for(int i=S;i<=T;++i) d[i]=inf,v[i]=0; 38 d[S]=0;v[S]=1;q.push(S); 39 while(!q.empty()) 40 { 41 int ff=q.front();q.pop();v[ff]=0; 42 for(int i=h[ff];i;i=e[i].ne) 43 { 44 int rr=e[i].v; 45 if(e[i].fl && d[rr]>d[ff]+e[i].c) 46 { 47 d[rr]=d[ff]+e[i].c; 48 if(!v[rr]) v[rr]=1,q.push(rr); 49 } 50 } 51 } 52 return d[T]!=inf; 53 } 54 int dfs(int u,int fl) 55 { 56 if(u==T || fl==0) return fl; 57 v[u]=1; 58 int get=0,f; 59 for(int i=h[u];i;i=e[i].ne) 60 { 61 int rr=e[i].v; 62 if(!v[rr] && e[i].fl && d[rr]==d[u]+e[i].c) 63 { 64 f=dfs(rr,min(fl,e[i].fl)); 65 if(f==0) continue; 66 get+=f;fl-=f; 67 e[i].fl-=f;e[i^1].fl+=f; 68 if(fl==0) break; 69 } 70 } 71 if(get==0) d[u]=inf; 72 return get; 73 } 74 void flow() 75 { 76 int cost=0,fl=0; 77 while(bfs()) 78 { 79 v[T]=1; 80 while(v[T]) 81 { 82 for(int i=S;i<=T;++i) v[i]=0; 83 int h=dfs(S,inf);fl+=h; 84 cost+=h*d[T]; 85 } 86 } 87 if(fl==b) cout<<"Yes"<<endl<<sum-cost; 88 else cout<<"No"<<endl<<fl; 89 } 90 int main() 91 { 92 n=read();m=read();a=read();b=read(); 93 tot=1;S=0;T=n*2+1; 94 for(int i=1,x;i<=n;++i) 95 { 96 x=read(); 97 add(i,i+n,x,inf); 98 } 99 for(int x,y,z,i=1;i<=m;++i) 100 { 101 x=read();y=read();z=read(); 102 if(x==y) continue; 103 add(x+n,y,z,inf);add(y+n,x,z,inf); 104 } 105 for(int x,y,i=1;i<=a;++i) 106 { 107 x=read();y=read(); 108 add(S,y,x,1); 109 } 110 for(int x,y,i=1;i<=b;++i) 111 { 112 x=read();y=read();sum+=x; 113 add(y+n,T,0,1); 114 } 115 flow(); 116 return 0; 117 }
转载自:https://www.luogu.org/blog/Tweetuzki/solution-p4237#
(?′?‵?)I L??????? 突然感觉好累的哦。

