week01-绪论

1、抽象数据模型

ADT Rational{

    数据对象：
        D={ e1, e2 | e1,e2属于ElemType类型} //ElemType是自定义的类型标识符

    数据关系：
        R={ <e1,e2> }  //e1为有理数的分子，e2为有理数的分母

    基本运算：
        InitRetion( *T, e1, e2)：构造有理数T，元素e1,e2分别被赋以分子、分母值

        DestroyRetion( *T )：销毁有理数T

        research( i, *T, e)：用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母

        modify( i, *T, e)：将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母

        add( *T1, *T2, *T3 )：有理数T1,T2相加,结果存入有理数T3

        minus( *T1, *T2, *T3 )：有理数T1,T2相减,结果存入有理数T3

        mult( *T1, *&T2, *T3 )：有理数T1,T2相乘,结果存入有理数T3

        division( *T1, *T2, *T3 )：有理数T1,T2相除,结果存入有理数T3

 }ADT Rational

2、头文件

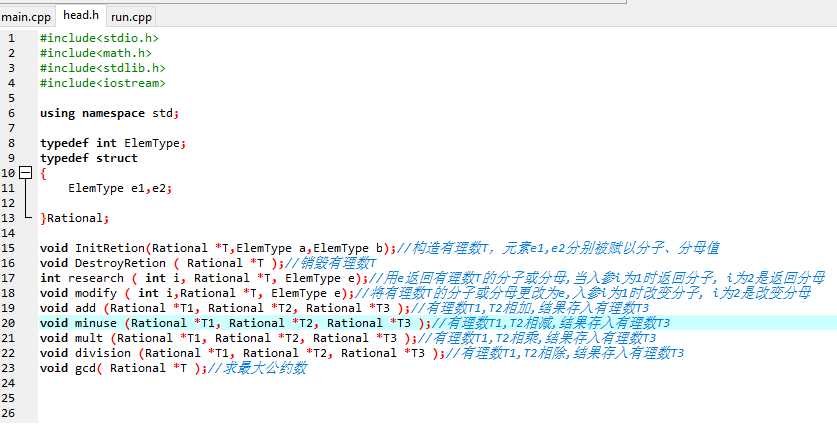
3、代码实现说明

• 1、构造有理数
  

• 2、分子（分母）的返回
  

• 3、分子（分母）的修改
  

• 4、求有理数之和
  

• 5、求有理数之差
  

• 6、求有理数之积
  

• 7、求有理数之商
  

• 8、约分（求最大公约数）
  

4、运行结果展示

• 样例
  

• 分母为零
  

• 负有理数
  

• sample
  

5、使用git上传代码到码云

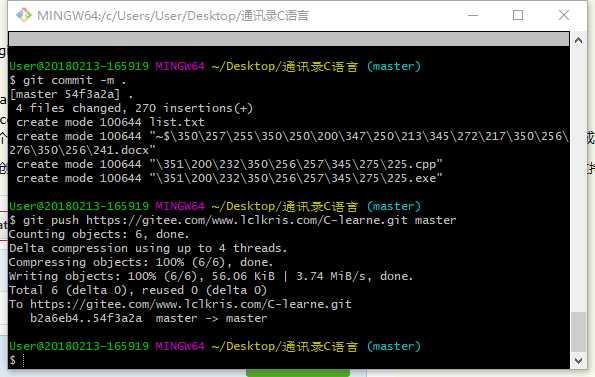
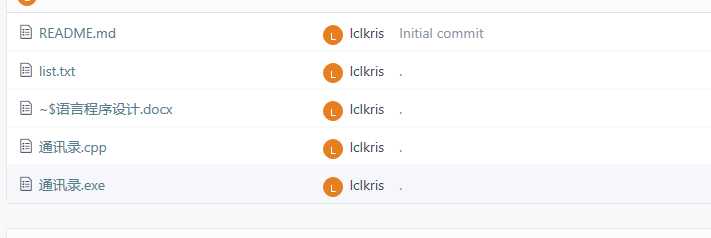
心得体会

• 明白了在 c 中函数的定义不能使用 &T