题目描述
给你一个图,每条边有一个权值。要求你选一些边,满足对于每条从\(1\)到\(n\)的路径上(可以不是简单路径)有且仅有一条被选中的边。问你选择的边的边权和最小值。
\(n\leq 100\)
题解
先把整张图分为两个集合\(S,T\),其中\(S\)是从原点开始BFS能够到达的点组成的集合,\(T\)是剩下的点组成的集合。
如果没有在一条路径上只能选一条边的限制,就是一个普通的网络流了。
我们看看什么情况下这个条件不会被满足。
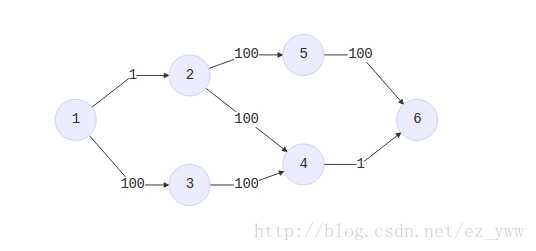
上面这个图中我们选择了\((1,2)\)和\((4,6)\)。\(S=\{1,3,4\},T=\{2,5,6\}\)。
可以发现如果多次从\(S\)走到\(T\)(比如上面这张图中\(1\rightarrow2\rightarrow4\rightarrow6\)),那么这些\(S\rightarrow T\)的边就都被选中同时在同一条路径上。所以不合法。
所以一旦走到\(T\)后就不能走回\(S\)。
如果一条边从\(T\)指向\(S\),那么这条边的反向边就满流了。
为了避免这种情况,只需要把反向边的容量设为\(\infty\)。
坑点:如果一条边的两个断点与\(S\)或\(T\)不连通,就不要连边。
时间复杂度:\(O(\)能过\()\)
代码
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<queue>
using namespace std;
typedef long long ll;
const ll inf=1e15;
namespace flow
{
int v[100010];
ll c[100010];
int t[100010];
int h[100010];
int n;
void add(int x,int y,ll a)
{
n++;
v[n]=y;
c[n]=a;
t[n]=h[x];
h[x]=n;
}
int d[100010];
int e[100010];
int op(int x)
{
return ((x-1)^1)+1;
}
int S,T;
queue<int> q;
int num;
int cur[100010];
void bfs()
{
memset(d,-1,sizeof d);
d[T]=0;
q.push(T);
int x,i;
while(!q.empty())
{
x=q.front();
q.pop();
e[d[x]]++;
for(i=h[x];i;i=t[i])
if(c[op(i)]&&d[v[i]]==-1)
{
d[v[i]]=d[x]+1;
q.push(v[i]);
}
}
}
ll dfs(int x,ll flow)
{
if(x==T)
return flow;
ll s=0,u;
for(int &i=cur[x];i;i=t[i])
if(c[i]&&d[v[i]]==d[x]-1)
{
u=dfs(v[i],min(flow,c[i]));
s+=u;
flow-=u;
c[i]-=u;
c[op(i)]+=u;
if(!flow)
return s;
}
e[d[x]]--;
if(!e[d[x]])
d[S]=num;
d[x]++;
e[d[x]]++;
cur[x]=h[x];
return s;
}
ll solve()
{
ll ans=0;
bfs();
memcpy(cur,h,sizeof h);
while(d[S]>=0&&d[S]<=num-1)
ans+=dfs(S,inf);
return ans;
}
}
void add(int x,int y,int c)
{
flow::add(x,y,c);
flow::add(y,x,inf);
}
int f[110][110];
int lx[2510];
int ly[2510];
int lz[2510];
int n,m;
int main()
{
#ifndef ONLINE_JUDGE
freopen("b.in","r",stdin);
freopen("b.out","w",stdout);
#endif
scanf("%d%d",&n,&m);
int i,j,k;
for(i=1;i<=m;i++)
{
scanf("%d%d%d",&lx[i],&ly[i],&lz[i]);
lx[i]++;
ly[i]++;
f[lx[i]][ly[i]]=1;
}
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
if(i!=k&&f[i][k])
for(j=1;j<=n;j++)
if(j!=i&&j!=k)
f[i][j]|=f[i][k]&&f[k][j];
for(i=1;i<=n;i++)
f[i][i]=1;
flow::S=1;
flow::T=n;
flow::num=n;
for(i=1;i<=m;i++)
if(f[1][lx[i]]&&f[ly[i]][n])
add(lx[i],ly[i],lz[i]);
ll ans=flow::solve();
if(ans>=inf)
printf("-1\n");
else
printf("%lld\n",ans);
return 0;
}