差分约束
差分约束是解决这样一类问题
给出\(n\)个形如\(x[j]-x[i]<=k\)的式子,求\(x[n]-x[1]\)的最大/最小值
思路
其实这个问题是挺套路的
我们把给出的式子变一下
\(x[j]-x[i]<=k\)
\(x[j]<=x[i]+k\)
我们不难联想到图论中最短路的性质
假设\(d[x]\)表示\(1\)到\(x\)的最短路
那么对于任意一条边\((u,v)\)
有\(d[v]<=d[u]+k\)(k表示边权)
可能有些抽象,举个例子
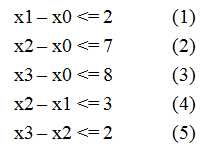
经过计算不难得到三个不等式
1.(3) x3 - x0 <= 8
2.(2) + (5) x3 - x0 <= 9
3.(1) + (4) + (5) x3 - x0 <= 7这样的话,我们在满足条件的情况下\(x[3]-x[0]\)最大为\(7\)
我们按上面的方法建出图
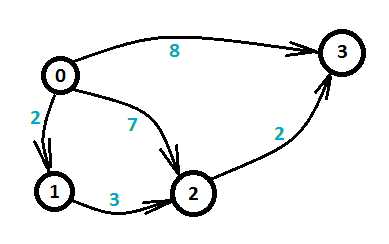
不难发现图中的最短路就是我们想要的答案!
难道这是巧合么?
肯定不是。仔细观察不难发现,我们连边的过程其实就是在转换不等式,求最短路其实就是求最小的限制条件。这样求出来的最短路即为满足条件的最大值
总结
这玩意儿其实挺套路的
如果你找出了题目中的限制条件,直接建图就好
最大值—>把所有式子整理为\(x[j]-x[i]<=k\),从\(i\)向\(j\)连一条边权为\(k\)的边,跑最短路
最小值—>把所有式子整理为\(x[j]-x[i]>=k\),从\(i\)向\(j\)连一条边权为\(k\)的边,跑最长路
在求解的时,因为经常要判断负环,所以选用SPFA算法
当一个点的入队次数超过\(n\)时必定出现负环
例题
几道水题
还有两道\(n\)年以前做的,没写题解
