题目:Luogu 1856
扫描线,将矩形拆成两条边分别为 +1 和 -1,计算无重叠部分的长度。
由于 update 区间 [a, b] 和 [b, c] 时会把 b 加两次,所以统一转换成 [a,b),累加长度的时候再将右端点右移。
需要注意,在覆盖一条边时,不能直接累加边的长度,像下图:
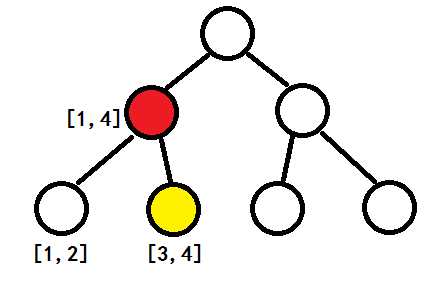
在覆盖边 [1,4] 前,[3,4] 已经累加过了,所以此时应该累计的是 [1,4] 的长度减去已经覆盖过的长度,然后再把 [1,4] 覆盖上;
相应的,在删除 [1,4] 这条边时,累计的是删除 [1,4] 前的长度 - 删除 [1,4] 后的长度。
其实就跟 矩形面积求并 这道题一样,线段树维护当前所有被覆盖的区间总长。
1 #include <cstdio> 2 #include <string> 3 #include <cstring> 4 #include <algorithm> 5 6 int read(); int abs(int); 7 8 struct Rectangle { 9 int x1, x2, y1, y2; 10 } rec[5005]; 11 12 struct Line { 13 int l, r, h, f; 14 bool operator < (const Line &cmp) const { 15 if (h == cmp.h) return f > cmp.f; 16 return h < cmp.h; 17 } 18 } line[10005]; 19 20 int hash[10005], cnt, sum[40005], tag[40005]; 21 22 int find(int x, int l, int r) { 23 while (l <= r) { 24 int mid = l + ((r - l) >> 1); 25 if (hash[mid] < x) l = mid + 1; 26 else if (hash[mid] == x) return mid; 27 else r = mid - 1; 28 } 29 } 30 31 void maintain(int cur, int l, int r) { 32 if (tag[cur]) sum[cur] = hash[r + 1] - hash[l]; 33 else if (l == r) sum[cur] = 0; 34 else sum[cur] = sum[cur << 1] + sum[cur << 1 | 1]; 35 } 36 37 void update(int cur, int l, int r, int L, int R, int flag) { 38 if (L <= l && r <= R) tag[cur] += flag; 39 else { 40 int mid = l + ((r - l) >> 1); 41 if (L <= mid) update(cur << 1, l, mid, L, R, flag); 42 if (mid < R) update(cur << 1 | 1, mid + 1, r, L, R, flag); 43 } 44 maintain(cur, l, r); 45 } 46 47 int solve() { 48 int res = 0; 49 std::sort(hash + 1, hash + cnt + 1); 50 std::sort(line + 1, line + cnt + 1); 51 for (int i = 1; i <= cnt; ++ i) { 52 int l = find(line[i].l, 1, cnt), 53 r = find(line[i].r, 1, cnt) - 1; 54 if (l <= r) { 55 int tmp = sum[1]; 56 update(1, 1, cnt, l, r, line[i].f); 57 res += abs(sum[1] - tmp); 58 } 59 } 60 return res; 61 } 62 63 int main() { 64 int n = read(), ans = 0; 65 for (int i = 1; i <= n; ++ i) { 66 rec[i].x1 = read(), rec[i].y1 = read(), 67 rec[i].x2 = read(), rec[i].y2 = read(); 68 hash[++cnt] = rec[i].x1, line[cnt].l = rec[i].x1, 69 line[cnt].r = rec[i].x2, line[cnt].h = rec[i].y1, line[cnt].f = 1; 70 hash[++cnt] = rec[i].x2, line[cnt].l = rec[i].x1, 71 line[cnt].r = rec[i].x2, line[cnt].h = rec[i].y2, line[cnt].f = -1; 72 } 73 ans += solve(); 74 cnt = 0; 75 for (int i = 1; i <= n; ++ i) { 76 hash[++cnt] = rec[i].y1, line[cnt].l = rec[i].y1, 77 line[cnt].r = rec[i].y2, line[cnt].h = rec[i].x1, line[cnt].f = 1; 78 hash[++cnt] = rec[i].y2, line[cnt].l = rec[i].y1, 79 line[cnt].r = rec[i].y2, line[cnt].h = rec[i].x2, line[cnt].f = -1; 80 } 81 ans += solve(); 82 printf("%d\n", ans); 83 return 0; 84 } 85 86 int abs(int x) { 87 if (x >= 0) return x; return -x; 88 } 89 90 int read() { 91 int x = 0, f = 1; 92 char c = getchar(); 93 while (!isdigit(c)) { 94 if (c == ‘-‘) f = -1; 95 c = getchar(); 96 } 97 while (isdigit(c)) { 98 x = (x << 3) + (x << 1) + (c ^ 48); 99 c = getchar(); 100 } 101 return x * f; 102 }
再说说暴力的做法,个人感觉这个不是很科学,是可以被卡掉的。
暴力就是考虑到 +1 的时候只累计由 0 变成 1 的区间,-1 的时候只累计由 1 变成 0 的区间,O(n^2) 累加 ans。
