week01-绪论

一、作业题目

仿照三元组或复数的抽象数据类型写出有理数抽象数据类型的描述 （有理数是其分子、分母均为整数且分母不为零的分数）。
有理数基本运算：

1. 构造有理数T，元素e1,e2分别被赋以分子、分母值
2. 销毁有理数T
3. 用e(引用类型参数)返回有理数T的分子或分母,当入参i为1时返回分子, i为2是返回分母。
4. 将有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母
5. 有理数T1,T2相加,结果存入有理数T3
6. 有理数T1,T2相减,结果存入有理数T3
7. 有理数T1,T2相乘,结果存入有理数T3
8. 有理数T1,T2相除,结果存入有理数T3
   实验要求：
9. 抽象数据类型名为Rational。
10. 有理数分母不能为负数或者0，类似输入请提示重输入。
11. 数据对象和数据运算的表示与数据操作的实现分离。表示用头文件完成，实现用CPP文件完成。Main.cpp文件实现数据输入输出。
12. 数据输入输出格式参考如下：
    输入：
    1 3 //T1的分子、分母
    1 2 //T2的分子、分母
    ** 输出：**
        5 6  //两个有理数相加
        -1 6  //两个有理数相减
        1 6  //两个有理数相乘
        2 3  //两个有理数相除
13. 程序应对异常输入或者出错必要处理和提示，比如提示：“分数是否需要约分等”。

二、实验

1、用ADT的抽象数据模型描述你的有理数数据类型。

   ADT Rationalnum{

   　　数据对象：D=｛e1,e2｜e1,e2均为整数且e2不为0｝

  　　 数据关系：R=｛<e1,e2>|e1是有理数的分子，e2是有理数的分母｝

   　　基本运算：

　　　　AssignRationalnum(&T,v1,v2)

　　　　操作结果：构造有理数T，元素e1,e2分别被赋予参数v1,v2的值

　　　　DestroyRationnum(&T)

　　　　操作结果：销毁有理数T

　　　　GetRationalnum(T,i,&e)

　　　　操作结果：e返回有理数T的分子或分母，i=1返回分子，i=2返回分母。

　　　　PutRationalnum（&T,i,e)

　　　　操作结果：有理数T的分子或分母更改为e,入参i为1时改变分子, i为2是改变分母

　　　　AddRationalnum(T1,T2,&T3）

　　　　操作结果：将T1，T2相加，结果存入T3

　　　　SubRationalnum(T1,T2,&T3)

　　　　操作结果：将T1，T2相减，结果存入T3

　　　　MulRational num(T1,T2,&T3)

　　　　操作结果：将T1，T2相乘，结果存入T3

　　　　DivRationalnum(T1,T2,&T3)

　　　　操作结果：将T1，T2相除，结果存入T3

｝ADT Rationalnum

2、数据结构，函数说明

3、代码实现说明

（1）求公因数。先判断分子的正负，再用辗转相除法求最大公因数

（2）有理数相加

（3）有理数相减

（4）有理数相乘  

（5）有理数相除

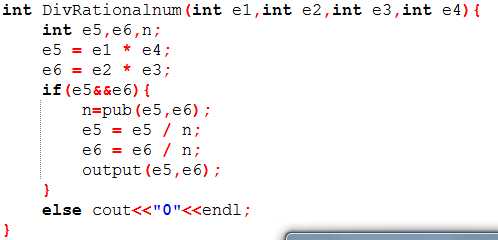
(6)输出结果

4、结果展示

（1）分子分母均为整数，且两个有理数的分子分母相同

（2）有理数分母为0时

（3）有理数分母为负数时

（4）有理数分子为0时

5、总结

(1) 、抽象数据类型是指一个数据模型以及定义在该模型上的一组操作。抽象数据类型的定义仅取决于它的一组逻辑特性，而与其在计算机内部如何表示和实现无关。

(2) 、数据结构分为逻辑结构和储存结构，对于一种数据结构，其逻辑结构总是唯一的，但它可能对应多种储存结构，并且在不同的储存结构中，同一运算的实现过程可能不同。

(3) 、逻辑结构数据元素间抽象化的相互关系与数据的存储无关，独立于计算机，它是从具体问题抽象出来的数学模型。储存结构是逻辑结构用计算机语言的实现或在计算机中的表示，其实就是逻辑结构在计算机中的储存方式，它是依赖于计算机语言的。