---恢复内容开始---
一、有理数的抽象数据模型
ADT Rational { 数据对象: D={e1,e2|e1,e2属于ElemType类型}//ElemType为自定义的整数集合类型 数据关系: R={<e1,e2>,e1是有理数分子,e2是有理数分母,并且e2!=0} 操作集: Init_Rational(&T,e1,e2) //操作结果:构造有理数T,并把元素e1,e2分别被赋值为有理数分子和分母 Destory_Rational(&T) //初始条件:有理数T已经存在 //操作结果:有理数T被销毁 Get_Rational(T,i,&e) //操作结果:用e返回有理数的分子或分母,i=1返回分子,i=2返回分母 PutRational(T,i,e) //操作结果:改变有理数的分子或分母的值为e,i=1改变分子,i=2改变分母 Add_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相加,结果保存在T3中 Sub_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相减,结果保存在T3中 Mul_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相乘,结果保存在T3中 Div_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相除,结果保存在T3中 }ADT Rational
二、头文件、函数说明
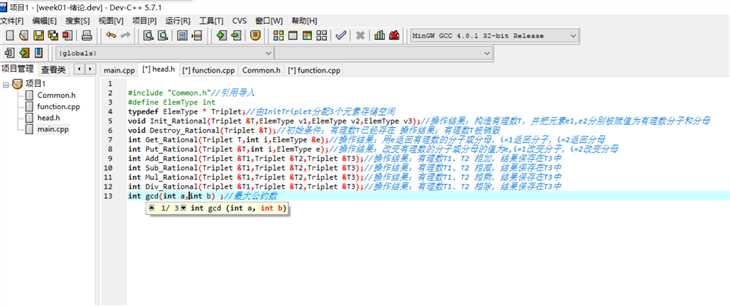
三、相关步骤的操作
1、有理数的构造,申请三元组空间

2、已构造的有理数的销毁

3、分子分母的返回

4、分子、分母的修改

5、两个有理数相加

6、两个有理数相减

7、两个有理数相乘

8、两个有理数相除

9、最大公约数的化简

四、运行结果的展示
五、总结:
1、很多东西都不会,C和C++有些地方的不同用法很容易会混淆。
2、从老师的参考代码中学到很多基础小知识,如#include "..."是为了实现引用导入的功能,还有一些宏定义。
3、以前习惯编一个个单独的cpp文件,现在突然用工程来做,有点不习惯,但是这样却能更清晰简明。
4、学会了一点点有关三元组的使用方法,明白其重要作用,对三元组这个抽象难懂的概念有了一个初步的认识。
5、上学期学的知识很多都忘了,这学期要努力补回来。
---恢复内容结束---
---恢复内容开始---
一、有理数的抽象数据模型
ADT Rational { 数据对象: D={e1,e2|e1,e2属于ElemType类型}//ElemType为自定义的整数集合类型 数据关系: R={<e1,e2>,e1是有理数分子,e2是有理数分母,并且e2!=0} 操作集: Init_Rational(&T,e1,e2) //操作结果:构造有理数T,并把元素e1,e2分别被赋值为有理数分子和分母 Destory_Rational(&T) //初始条件:有理数T已经存在 //操作结果:有理数T被销毁 Get_Rational(T,i,&e) //操作结果:用e返回有理数的分子或分母,i=1返回分子,i=2返回分母 PutRational(T,i,e) //操作结果:改变有理数的分子或分母的值为e,i=1改变分子,i=2改变分母 Add_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相加,结果保存在T3中 Sub_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相减,结果保存在T3中 Mul_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相乘,结果保存在T3中 Div_Rational(T1,T2,&T3) //操作结果:有理数T1、T2 相除,结果保存在T3中 }ADT Rational
二、头文件、函数说明

三、相关步骤的操作
1、有理数的构造,申请三元组空间

2、已构造的有理数的销毁

3、分子分母的返回

4、分子、分母的修改

5、两个有理数相加

6、两个有理数相减

7、两个有理数相乘

8、两个有理数相除

9、最大公约数的化简

四、运行结果的展示


五、总结:
1、很多东西都不会,C和C++有些地方的不同用法很容易会混淆。
2、从老师的参考代码中学到很多基础小知识,如#include "..."是为了实现引用导入的功能,还有一些宏定义。
3、以前习惯编一个个单独的cpp文件,现在突然用工程来做,有点不习惯,但是这样却能更清晰简明。
4、学会了一点点有关三元组的使用方法,明白其重要作用,对三元组这个抽象难懂的概念有了一个初步的认识。
5、上学期学的知识很多都忘了,这学期要努力补回来。
---恢复内容结束---
