众所周知,贝叶斯定理是一种在已知其他概率的情况下求概率的方法:
首先,对于贝叶斯定理,还是要先了解各个概率所对应的事件。
P(A|B) 是在 B 发生的情况下 A 发生的概率;
P(A) 是 A 发生的概率;
P(B|A) 是在 A 发生的情况下 B 发生的概率;
P(B) 是 B 发生的概率。
贝叶斯法则的原理
根据文氏图,可以很清楚地看到在事件B发生的情况下,事件A发生的概率就是P(A∩B)除以P(B)。
因此,
同理可得,
所以,
即,
这就是条件概率的计算公式。
全概率公式
由于后面要用到,所以除了条件概率以外,这里还要推导全概率公式。
假定样本空间S,是两个事件A与A‘的和。

上图中,红色部分是事件A,绿色部分是事件A‘,它们共同构成了样本空间S。
在这种情况下,事件B可以划分成两个部分。

即
在上一节的推导当中,我们已知
所以,
这就是全概率公式。它的含义是,如果A和A‘构成样本空间的一个划分,那么事件B的概率,就等于A和A‘的概率分别乘以B对这两个事件的条件概率之和。
将这个公式代入上一节的条件概率公式,就得到了条件概率的另一种写法:
病人分类的例子
让我从一个例子开始讲起,你会看到贝叶斯分类器很好懂,一点都不难。某个医院早上收了六个门诊病人,如下表。
| 症状 | 职业 | 疾病 |
| 打喷嚏 | 护士 | 感冒 |
| 打喷嚏 | 农夫 | 过敏 |
| 头疼 | 建筑工人 | 脑震荡 |
| 头疼 | 建筑工人 | 感冒 |
| 打喷嚏 | 教师 | 感冒 |
| 头疼 | 教师 | 脑震荡 |
现在又来了第七个病人,是一个打喷嚏的建筑工人。请问他患上感冒的概率有多大? 根据贝叶斯定理:
P(A|B) = P(B|A) P(A) / P(B)
可得:
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏x建筑工人|感冒) x P(感冒)
/ P(打喷嚏x建筑工人)
假定"打喷嚏"和"建筑工人"这两个特征是独立的,因此,上面的等式就变成了
P(感冒|打喷嚏x建筑工人)
= P(打喷嚏|感冒) x P(建筑工人|感冒) x P(感冒)
/ P(打喷嚏) x P(建筑工人)
这是可以计算的。
P(感冒|打喷嚏x建筑工人)
= 0.66 x 0.33 x 0.5 / 0.5 x 0.33
= 0.66
因此,这个打喷嚏的建筑工人,有66%的概率是得了感冒。同理,可以计算这个病人患上过敏或脑震荡的概率。比较这几个概率,就可以知道他最可能得什么病。
这就是贝叶斯分类器的基本方法:在统计资料的基础上,依据某些特征,计算各个类别的概率,从而实现分类。
贝叶斯滤波器
首先,BF是什么?
BF是依据机器人传感器获取的观测数据,利用Bayes公式(概率论)去估计机器人的状态的一种手段。
这里的关键点在于,BF假设了机器人当前的状态服从某一个概率分布,将机器人状态估计问题建模为一个概率分布的估计问题,从而利用概率论的数学工具来解决机器人的状态估计。
那么为什么要用BF呢?
这是因为,机器人的运动模型以及传感器的观测模型常常受到噪声干扰,而这种噪声都是随机性的。这样建模就可以有利于我们把噪声的分布、统计特性给估计出来,从而去除噪声,得到真实观测以及真实状态。
那么,BF具体是怎么对机器人状态估计问题建模的呢?
举一个例子,我做了一只小狗机器人,它身上装了GPS,可以时刻返回小狗机器人的位置。为了遥控它,我还给它装了一个遥控接收装置(根据小狗之前在的位置加上遥控量,也能算出小狗的位置)。但是,我遇到两个问题。一是,我花的钱太少了,买到GPS不太准,本来小狗应该在(5,3)的位置,但是测量的结果却是(5.1,2.8)。二是,小狗机器人接收到指令是前进1米,但是实际走的却可能是0.98米。小狗机器人的观测过程和运动过程中都存在噪声的干扰,这使得我想要知道我的小狗跑到哪里变得很困难,需要借助滤波手段来估计小狗位置。
基于这个例子,由于受到噪声污染,小狗机器人位置和GPS的观测可以被建模为概率分布,以表征其不确定性,即:
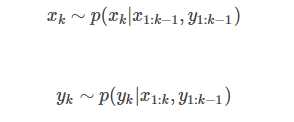
其中,x,yx,y分别代表小狗机器人的位置,以及GPS测量到的小狗机器人的位置。
下标代表的是时间。
这两个式子分别可以称为小狗机器人系统的动态模型(通常用状态方程描述,即从一个状态如何变化到另一个状态)和观测模型(通常用观测方程描述,即当前状态下能够获取到怎么样的观测)
表达的意思是:k时刻小狗的位置服从以1到k-1时刻的小狗位置以及1到k-1时刻的GPS测量值为条件的一个概率分布
另外,k时刻GPS的测量值服从以1到k时刻的小狗位置以及1到k-1时刻的GPS测量值为条件的一个概率分布。
参考资料:
机器学习(10)之趣味案例理解朴素贝叶斯
https://mp.weixin.qq.com/s/s0v_afLVqtJhZyn3qHlseQ
可怕的贝叶斯:
http://dy.163.com/v2/article/detail/CU0MJOCV05118CTM.html
算法——贝叶斯:
https://www.cnblogs.com/skyme/p/3564391.html
贝叶斯滤波器:
