什么是最长上升子序列,最长上升子序列就是在一段数字中最长按严格递增数列,不一定要连续
最长上升子序列有3种解法,但后面两种的时间复杂度都是nlogn,所以只列出其中比较常用的一种
而另一种就是用动态规划来做。
第一种,永远dp来做:
例如给出了2 5 3 4 1 7 6这了一段数字,这段数字存在了a数组当中
其中最长上升子序列是4
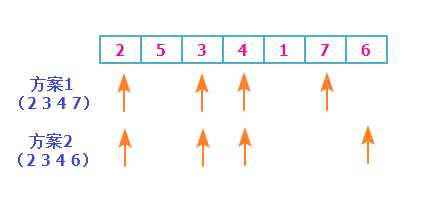
我们先建立另一个数组F,F的作用是储存从1到i的最长上升子序列数。
当aj<ai(j<i),且当F[j]+1>F[i]时,F[j]+1>F[i]。对于每一个数都可以建立这样的求解方式
所以,要得出最终答案需要枚举前i个数字,即O(n^2)。
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int maxn = 103; const int INF=0x7f7f7f7f; int a[maxn],F[maxn]; int n,ans=-INF; int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); F[i]=1; } for(int i=1;i<=n;i++) for(int j=1;j<i;j++) if(a[j]<a[i])F[i]=max(F[i],F[j]+1); for(int i=1;i<=n;i++) ans=max(ans,F[i]); printf("%d\n",ans); return 0;
}
第二种方法:(此段来自http://blog.csdn.net/George__Yu/article/details/75896330)
利用二分进行查找的方法,我们新建立一个low数组,ow[i]表示长度为i的LIS结尾元素的最小值。对于一个上升子序列,显然其结尾元素越小,越有利于在后面接其他的元素,也就越可能变得更长。所以我们只需要对low进行维护就行。
那么,怎么维护low数组呢?
对于每一个a[i],如果a[i]能接到LIS后面,就接上去;否则,就用a[i]取更新low数组。具体方法是,在low数组中找到第一个大于等于a[i]的元素low[j],用a[i]去更新low[j]。如果从头到尾扫一遍low数组的话,时间复杂度仍是O(n^2)。我们注意到low数组内部一定是单调不降的,所有我们可以二分low数组,找出第一个大于等于a[i]的元素。二分一次low数组的时间复杂度的O(lgn),所以总的时间复杂度是O(nlogn)。
#include <iostream> #include <cstdio> #include <algorithm> #include <cstdlib> #include <cstring> #include <cmath> using namespace std; const int maxn =300003,INF=0x7f7f7f7f; int low[maxn],a[maxn]; int n,ans; int binary_search(int *a,int r,int x) //二分查找,返回a数组中第一个>=x的位置 { int l=1,mid; while(l<=r) { mid=(l+r)>>1; if(a[mid]<=x) l=mid+1; else r=mid-1; } return l; } int main() { scanf("%d",&n); for(int i=1;i<=n;i++) { scanf("%d",&a[i]); low[i]=INF;//由于low中存的是最小值,所以low初始化为INF } low[1]=a[1]; ans=1;//初始时LIS长度为1 for(int i=2;i<=n;i++) { if(a[i]>=low[ans])//若a[i]>=low[ans],直接把a[i]接到后面 low[++ans]=a[i]; else //否则,找到low中第一个>=a[i]的位置low[j],用a[i]更新low[j] low[binary_search(low,ans,a[i])]=a[i]; } printf("%d\n",ans);//输出答案 return 0; }
