http://www.lydsy.com/JudgeOnline/problem.php?id=4872
一种最优解是 从大到小灯有亮的就灭掉
最优解是唯一的,且关灯的顺序没有影响
最优解 对每个开关至多操作1次,(连带着的灯的亮灭改变不算)
设最优解 需要操作cnt次,那么就有cnt盏灯是正确的选择
设 f[i] 表示 有i种正确的选择 变为 有i-1种正确的选择 的 期望次数
那么在n盏灯中,有i盏灯操作1次 就可以 减少一次正确选择
有n-i盏灯是错误的选择,选了它还要把它还原,还原它也是一种正确选择,就是f[i+1];一次错误的选择 做了一次 操作 就是1;当然也要变成i-1种正确选择
所以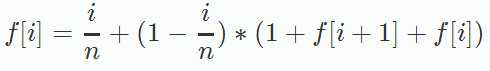
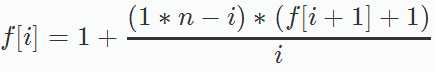
边界:f[n]=1,随便选择任何一盏灯都是正确选择
#include<cstdio> #include<vector> using namespace std; #define N 100001 bool a[N]; vector<int>V[N]; int f[N],inv[N]; const int mod=100003; int main() { int n,k; scanf("%d%d",&n,&k); for(int i=1;i<=n;++i) scanf("%d",&a[i]); for(int i=1;i<=n;++i) for(int j=i;j<=n;j+=i) V[j].push_back(i); int cnt=0,ans=0; for(int i=n;i;--i) if(a[i]) { cnt++; int m=V[i].size(); for(int j=0;j<m;++j) a[V[i][j]]^=1; } if(cnt<=k) ans=cnt; else { inv[1]=1; for(int i=2;i<n;++i) inv[i]=1LL*(mod-mod/i)*inv[mod%i]%mod; f[n]=1; for(int i=n-1;i;--i) f[i]=(1+1LL*(n-i)*(1+f[i+1])*inv[i])%mod; for(int i=cnt;i>k;--i) ans=(ans+f[i])%mod; ans=(ans+k)%mod; } for(int i=2;i<=n;++i) ans=1LL*ans*i%mod; printf("%d",ans); }
4872: [Shoi2017]分手是祝愿
Time Limit: 20 Sec Memory Limit: 512 MBSubmit: 466 Solved: 304
[Submit][Status][Discuss]
Description
Zeit und Raum trennen dich und mich.
时空将你我分开。B 君在玩一个游戏,这个游戏由 n 个灯和 n 个开关组成,给定这 n 个灯的初始状态,下标为
从 1 到 n 的正整数。每个灯有两个状态亮和灭,我们用 1 来表示这个灯是亮的,用 0 表示这个灯是灭的,游戏
的目标是使所有灯都灭掉。但是当操作第 i 个开关时,所有编号为 i 的约数(包括 1 和 i)的灯的状态都会被
改变,即从亮变成灭,或者是从灭变成亮。B 君发现这个游戏很难,于是想到了这样的一个策略,每次等概率随机
操作一个开关,直到所有灯都灭掉。这个策略需要的操作次数很多, B 君想到这样的一个优化。如果当前局面,
可以通过操作小于等于 k 个开关使所有灯都灭掉,那么他将不再随机,直接选择操作次数最小的操作方法(这个
策略显然小于等于 k 步)操作这些开关。B 君想知道按照这个策略(也就是先随机操作,最后小于等于 k 步,使
用操作次数最小的操作方法)的操作次数的期望。这个期望可能很大,但是 B 君发现这个期望乘以 n 的阶乘一定
是整数,所以他只需要知道这个整数对 100003 取模之后的结果。
Input
第一行两个整数 n, k。
接下来一行 n 个整数,每个整数是 0 或者 1,其中第 i 个整数表示第 i 个灯的初始情况。
1 ≤ n ≤ 100000, 0 ≤ k ≤ n;
Output
输出一行,为操作次数的期望乘以 n 的阶乘对 100003 取模之后的结果。
Sample Input
4 0
0 0 1 1
0 0 1 1
Sample Output
512
