题面:
一句话,就是让你求$\mu\left(i^2\right)$以及$\varphi\left(i^2\right)$的前缀和
思路:
第一问,瞪了一会儿恍然大悟:这不就是1吗......
因为对于$\mu\left(i^2\right)$,$i^2=i\ast i$,那么$\mu\left(i^2\right)$在$i\neq1$的时候值都是0
所以第一问输出1就好了......
接下来看第二问
这一问中解决$\varphi\left(i^2\right)$是关键,因为这东西是个积性函数,可以套进杜教筛里面,而一旦进了杜教筛这题就解决了
当前的关键,是找到杜教筛套路式子中的$g\left(x\right)
我当时想了半天,准备从$\varphi$函数的本质下手,奈何能力不足,就参考了一下某度上的结果,然后看到了这个东西:
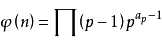
发现,当$n$变成$n^2$的时候,右边的每一个质数$p$的指数都上升了$a_p$
也就是说,$\varphi\left(i^2\right)=\varphi\left(i\right)\ast i$
美!滋!滋!
所以我们只要设$g\left(x\right)=x$,然后套用杜教筛套路:
$ g\left(1\right)S\left(n\right)=\sum_{i=1}^{n}\left(g\ast f\right)\left(i\right)-\sum_{i=2}^{n}g\left(i\right)S\left(\frac ni\right) $
此时g和f函数的卷积等于id
$ S\left(n\right)=\sum_{i=1}^{n}i-\sum{i=2}^{n}iS\left(\frac ni\right) $
然后就递归记忆化AC
Code:
1 #include<iostream> 2 #include<cstring> 3 #include<algorithm> 4 #include<cstdio> 5 #include<map> 6 #define ll long long 7 ll MOD=1e9+7,inv6=166666668; 8 using namespace std; 9 inline ll read(){ 10 ll re=0,flag=1;char ch=getchar(); 11 while(ch>‘9‘||ch<‘0‘){ 12 if(ch==‘-‘) flag=-1; 13 ch=getchar(); 14 } 15 while(ch>=‘0‘&&ch<=‘9‘) re=(re<<1)+(re<<3)+ch-‘0‘,ch=getchar(); 16 return re*flag; 17 } 18 ll tot,pri[2000010],phi[2000010];bool vis[2000010]={0}; 19 void init(){ 20 ll i,j,k;phi[1]=1;vis[1]=1; 21 for(i=2;i<=2000000;i++){ 22 if(!vis[i]){ 23 pri[++tot]=i;phi[i]=i-1; 24 } 25 for(j=1;j<=tot;j++){ 26 k=i*pri[j];if(k>2000000) break; 27 vis[k]=1; 28 if(i%pri[j]==0){ 29 phi[k]=phi[i]*pri[j]%MOD; 30 break; 31 } 32 phi[k]=phi[i]*phi[pri[j]]%MOD; 33 } 34 } 35 for(i=1;i<=2000000;i++) phi[i]=(i*phi[i]%MOD+phi[i-1])%MOD; 36 } 37 map<ll,ll>m; 38 ll sum(ll l,ll r){return (r-l+1)*(r+l)/2%MOD%MOD;} 39 ll sum2(ll x){x%=MOD;return x*(x+1)%MOD*(2*x+1)%MOD*inv6%MOD;} 40 ll S(ll x){ 41 if(x<=2000000) return phi[x]; 42 if(m[x]) return m[x]; 43 ll i,j,re=sum2(x); 44 for(i=2;i<=x;i=j+1){ 45 j=x/(x/i); 46 re-=sum(i,j)*S(x/i)%MOD;re%=MOD; 47 } 48 return m[x]=(re+MOD)%MOD; 49 } 50 int main(){ 51 ll i,j,n;init(); 52 n=read();puts("1"); 53 printf("%lld\n",S(n)); 54 }
