前面介绍的链表,栈,队列都是一种顺序容器,访问元素的时候都是通过位置来访问的。如果想要通过值的方式来获取数据,只能通过遍历的方式。这在时间上消耗比较大。而二叉树可以做到不用遍历就可以通过值的方式来获取数据。二叉树是按值来保存元素,也按值来访问元素。
二叉树的相关术语:
树的结点:包含一个数据元素及若干指向子树的分支;
孩子结点:结点的子树的根称为该结点的孩子;
双亲结点:B 结点是A 结点的孩子,则A结点是B 结点的双亲;
兄弟结点:同一双亲的孩子结点; 堂兄结点:同一层上结点;
祖先结点: 从根到该结点的所经分支上的所有结点子孙结点:以某结点为根的子树中任一结点都称为该结点的子孙
结点层:根结点的层定义为1;根的孩子为第二层结点,依此类推;
树的深度:树中最大的结点层
结点的度:结点子树的个数
树的度: 树中最大的结点度。
叶子结点:也叫终端结点,是度为 0 的结点;
分枝结点:度不为0的结点;
有序树:子树有序的树,如:家族树;
无序树:不考虑子树的顺序;[3]
二叉树的定义:
二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。二叉树常被用于实现二叉查找树和二叉堆。
二叉树的每个结点至多只有二棵子树(不存在度大于2的结点),二叉树的子树有左右之分,次序不能颠倒。二叉树的第i层至多有2^(i-1)个结点;深度为k的二叉树至多有2^k-1个结点;对任何一棵二叉树T,如果其终端结点数为n_0,度为2的结点数为n_2,则n_0=n_2+1。
若设二叉树的高度为h,除第 h 层外,其它各层 (1~h-1) 的结点数都达到最大个数,第h层有叶子节点,并且叶子结点都是从左到右依次排布,这就是完全二叉树。
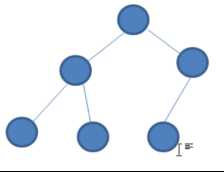
一棵深度为k,且有2^k-1个节点的二叉树,称为满二叉树。
这种树的特点是每一层上的节点数都是最大节点数。
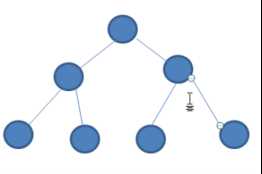
而在一棵二叉树中,除最后一层外,若其余层都是满的,并且最后一层或者是满的,或者是在右边缺少连续若干节点,则此二叉树为完全二叉树。

具有n个节点的完全二叉树的深度为log2n+1。深度为k的完全二叉树,至少有2^(k-1)个节点,至多有2^k-1个节点。
二叉树的性质:
性质1:二叉树第i层上的结点数目最多为 2{i-1} (i≥1)。
性质2:深度为k的二叉树至多有2{k}-1个结点(k≥1)。
性质3:包含n个结点的二叉树的高度至少为log2 (n+1)。
性质4:在任意一棵二叉树中,若终端结点的个数为n0,度为2的结点数为n2,则n0=n2+1
完全二叉树的性质:假设有n个节点
如果i=1,则结点i是二叉树的根
如果i>1,则其双亲结点是i/2
如果2i<=n,则结点的左孩子为2i
如果2i>n,则结点i无左孩子
如果2i+1<=n, 则结点i的右孩子为2i+1
如果2i+1>n,则结点i无右孩子。
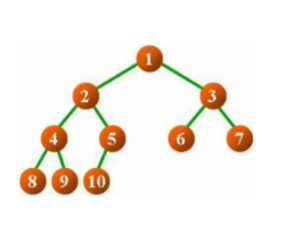
遍历二叉树:
有三种遍历方式:1 先根序遍历 2 中根序遍历 3 后根序遍历
1 先根序遍历:先访问根结点,而后以同样方式顺序遍历左子树和右子树
2 中根序遍历:先以同样方式遍历左子树,然后访问根结点,最后再以同样的方式遍历右子树
3 后根序遍历:先以同样方式遍历左右子树,最后访问根结点
比如下面这张图:
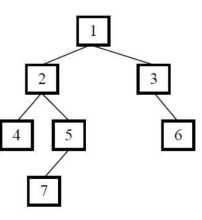
先根序遍历的顺序 1->2->4->5->7->3->6
中根序遍历的顺序 4->2->7->5->1->3->6
后根序遍历的顺序 4->7->5->2->6->3->1
下面来看下如何创建二叉树和层次遍历一个二叉树
class Tree():
def __init__(self):
self.root=None
self.result=[]
self.q=[]
def add(self,elem):
node=Node(elem)
if self.root is None:
self.root=node
else:
q=[self.root]
while True:
pop_node=q.pop(0)
if pop_node.lchild is None:
pop_node.lchild=node
return
if pop_node.rchild is None:
pop_node.rchild = node
return
else:
q.append(pop_node.lchild)
q.append(pop_node.rchild)
#基于队列的层次遍历
def level_print(self):
if self.root == None:
return ‘empyt tree‘
self.q.append(self.root)
while True:
if len(self.q) > 0:
current = self.q.pop(0)
self.result.append(current.elem)
if current.lchild != None:
self.q.append(current.lchild)
if current.rchild != None:
self.q.append(current.rchild)
else:
break
print self.result
if __name__=="__main__":
elems=range(10)
tree=Tree()
for elem in elems:
tree.add(elem)
tree.level_print()
打印结果:
/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter6.py
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
先根遍历,中根遍历,后根遍历的实现
def pre_order(tree):
if tree == None:
return ‘empyt tree‘
print tree.elem
pre_order(tree.lchild)
pre_order(tree.rchild)
def middle_order(tree):
if tree == None:
return ‘empty tree‘
middle_order(tree.lchild)
print tree.elem
middle_order(tree.rchild)
def post_order(tree):
if tree == None:
return ‘empty tree‘
post_order(tree.lchild)
post_order(tree.rchild)
print tree.elem
运行结果:
/usr/bin/python2.7 /home/zhf/py_prj/data_struct/chapter6.py
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
pre_order
0
1
3
7
8
4
9
2
5
6
middle_order
7
3
8
1
9
4
0
5
2
6
post_order
7
8
3
9
4
1
5
6
2
0
