3996: [TJOI2015]线性代数

Time Limit: 10 Sec Memory Limit: 128 MB
Submit: 1850 Solved: 1097
[Submit][Status][Discuss]

Description

给出一个NN的矩阵B和一个1N的矩阵C。求出一个1N的01矩阵A.使得
D=（AB-C）*A^T最大。其中A^T为A的转置。输出D

Input

第一行输入一个整数N，接下来N行输入B矩阵，第i行第J个数字代表Bij.
接下来一行输入N个整数，代表矩阵C。矩阵B和矩阵C中每个数字都是不超过1000的非负整数。

Output

输出最大的D

Sample Input

3

1 2 1

3 1 0

1 2 3

2 3 7

Sample Output

2

HINT

1<=N<=500

Source

题解

分析一下就会发现
\[Ans = \sum_{i=1}^{n}\sum_{j=1}^{n}(A_i \times B{_i}{_j} \times A_j - C_i \times A_i)\]
即：
选\(i\)并且选\(j\)，才能获得\(B{_i}{_j}\)的价值
选\(i\)会损失\(C_i\)的价值
选\(j\)会损失\(C_j\)的价值

如果做过\(BZOJ2127\)或者\(BZOJ2132\)，就会觉得这题真水。
对于i,j,这样建模：

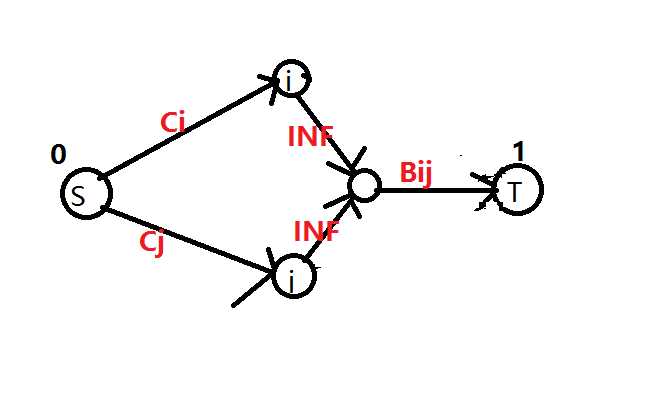
一遍过

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <algorithm>
#include <map>
#include <cmath>
inline int max(int a, int b){return a > b ? a : b;}
inline int min(int a, int b){return a < b ? a : b;}
inline int abs(int x){return x < 0 ? -x : x;}
inline void swap(int &x, int &y){int tmp = x;x = y;y = tmp;}
inline void read(int &x)
{
    x = 0;char ch = getchar(), c = ch;
    while(ch < '0' || ch > '9') c = ch, ch = getchar();
    while(ch <= '9' && ch >= '0') x = x * 10 + ch - '0', ch = getchar();
    if(c == '-') x = -x;
}
const int INF = 0x3f3f3f3f;
struct Edge
{
    int u,v,w,nxt;
    Edge(int _u, int _v, int _w, int _nxt){u = _u;v = _v;w = _w;nxt = _nxt;}
    Edge(){}
}edge[3000010];
int head[1000010], cnt = 1, S, T, cur[1000010], q[1000010], he, ta, h[1000010], ans;
inline void insert(int a, int b, int c)
{
    edge[++ cnt] = Edge(a, b, c, head[a]), head[a] = cnt;
    edge[++ cnt] = Edge(b, a, 0, head[b]), head[b] = cnt;
}
bool bfs()
{
    memset(h, -1, sizeof(h)), h[S] = 0, he = ta = 0, q[ta ++] = S;
    while(he < ta)
    {
        register int now = q[he ++];
        for(register int pos = head[now];pos;pos = edge[pos].nxt)
        {
            register int v = edge[pos].v;
            if(edge[pos].w && h[v] == -1)
                h[v] = h[now] + 1, q[ta ++] = v;
        }
    }
    return h[T] != -1;
}
int dfs(int x, int f)
{
    if(x == T || f == 0) return f;
    int used = 0, w;
    for(register int& pos = cur[x];pos;pos = edge[pos].nxt)
    {
        register int v = edge[pos].v;
        if(h[v] == h[x] + 1 && edge[pos].w > 0)
        {
            w = dfs(v, min(edge[pos].w, f - used));
            if(w > 0)
                edge[pos].w -= w, edge[pos ^ 1].w += w, used += w;
            if(used == f) return f;
        }
    }
    if(!used) h[x] = -1;
    return used;
}
void dinic()
{
    while(bfs()) 
    {
        memcpy(cur, head, sizeof(head));
        ans += dfs(S, INF);
    }
}
int n, tot, sum, tmp;
int main()
{
    read(n);
    tot = n;
    S = ++ tot, T = ++ tot;
    for(int i = 1;i <= n;++ i)
        for(int j = 1;j <= n;++ j)
        {
            read(tmp);
            ++ tot;
            insert(i, tot, INF);
            insert(j, tot, INF);
            insert(tot, T, tmp);
            sum += tmp;
        }
    for(int i = 1;i <= n;++ i) 
    { 
        read(tmp);
        insert(S, i, tmp);
    } 
    dinic();
    printf("%d", sum - ans);
    return 0;
}