第二节，神经网络中反向传播四个基本公式证明——BackPropagation

参考文章

神经网络基础

Neural Networks and Deep Learning.       Michael A. Nielsen

 一文弄懂神经网络中的反向传播法：讲的很详细，用实例演示了反向传播法中权重的更新过程，但是未涉及偏置的更新

假设一个三层的神经网络结构图如下：

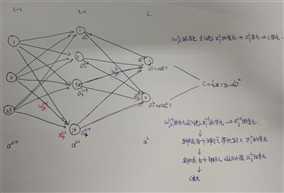
对于一个单独的训练样本x其二次代价函数可以写成：

          C = 1/2|| y - a^L||² = 1/2∑_j(y_j - a_j^L)²

          a_j^L=σ(z_j^L)

          z_j^l = ∑_kω_jk^la_k^l-1 + b_j^l

代价函数C是a_j^L的函数，a_j^L又是z_j^L的函数，z_j^L又是ω_jk^L的函数，同时又是a_k^L-1的函数......

证明四个基本方程(BP1-BP4)，所有这些都是多元微积分的链式法则的推论

            δ_j^L = (?C/?a_j^L)σ‘(z_j^L)                                                         (BP1)

             δ_j^l = ∑_k ω_kj^l+1δ_k^l+1σ‘(z_j^l)                                                    (BP2)

　　　   ?C/?ω_jk^l = δ_j^la_k^l-1                                                                           (BP3)

              ?C/?b_j^l = δ_j^l                                                                                      (BP4)

1.让我们从方程(BP1)开始，它给出了输出误差δ^L的表达式。

            δ_j^L = ?C/?z_j^L

    应用链式法则，我们可以就输出激活值的偏导数的形式重新表示上面的偏导数：

              δ_j^L = ∑_k (?C/?a_k^L)(?a_k^L/?z_j^L)

    这里求和是在输出层的所有神经元k上运行的，当然，第k^th个神经元的输出激活值a_k^L只依赖于当k=j时第j^th个神经元的带权输入z_j^L。所以当k≠j

    时，?a_k^L/?z_j^L=0。结果简化为：

               δ_j^L = (?C/?a_j^L)(?a_j^L/?z_j^L)

    由于a_j^L=σ(z_j^L)，右边第二项可以写成σ‘(z_j^L)，方程变成

                δ_j^L = (?C/?a_j^L)σ‘(z_j^L)

2.证明BP2，它给出了下一层误差δ^l+1的形式表示误差δ^l。为此我们要以δ_k^l+1=?C/?z_k^l+1的形式重写 δ_j^l = ?C/?z_j^l

              δ_j^l = ?C/?z_j^l

                   =∑_k (?C/?z_k^l+1)(?z_k^l+1/?z_j^l)

                  =∑_k (?z_k^l+1/?z_j^l)δ_k^l+1

     这里最后一行我们交换了右边的两项，并用δ_k^l+1的定义带入。为此我们对最后一行的第一项求值，

     注意：

             z_k^l+1 = ∑_jω_kj^l+1a_j^l + b_k^l+1 =  ∑_jω_kj^l+1σ(z_j^l) + b_k^l+1 

     做微分得到

            ?z_k^l+1 /?z_j^l = ω_kj^l+1σ‘(z_j^l)

     带入上式:

            δ_j^l = ∑_k ω_kj^l+1δ_k^l+1σ‘(z_j^l)

3.证明BP3。计算输出层?C/?ω_jk^L：

            ?C/?ω_jkL = ∑_m (?C/?a_m^L)(?a_m^L/?ω_jk^L )

     这里求和是在输出层的所有神经元k上运行的，当然，第k^th个神经元的输出激活值a_m^L只依赖于当m=j时第j^th个神经元的输入权重ω_jk^L。所以当k≠j

　  时，?a_m^L/?ω_jk^L=0。结果简化为：

　　    ?C/?ω_jk^L = (?C/?a_j^L)(?a_j^L/?z_j^L)*(?z_j^L/?ω_jk^L)

                         = δ_j^La_k^L-1

       计算输入层上一层(L-1):

           ?C/?ω_jk^L-1= (∑_m(?C/?a_m^L)(?a_m^L/?z_m^L)(?z_m^L/?a_j^L-1))(/?a_j^L-1/?z_j^L-1)(?z_j^L-1/?ω_jk^L-1)

                           = (∑_mδ_m^Lω_mj^L)σ‘(z_j^L-1)a_k^L-2

                           = δ_j^L-1a_k^L-2

      对于处输入层的任何一层(l)：

            ?C/?ω_jk^l = (?C/?z_j^l )(?z_j^l/?ω_jk^l ) = δ_j^la_k^l-1

4.证明BP4。计算输出层?C/?b_j^L：

            ?C/?b_j^L = ∑_m (?C/?a_m^L)(?a_m^L/?b_j^L )

     这里求和是在输出层的所有神经元k上运行的，当然，第k^th个神经元的输出激活值a_m^L只依赖于当m=j时第j^th个神经元的输入权重b_j^L。所以当k≠j

　  时，?a_m^L/?b_j^L=0。结果简化为：

　　    ?C/?b_j^L = (?C/?a_j^L)(?a_j^L/?z_j^L)*(?z_j^L/?b_j^L)

                         = δ_j^L

       计算输入层上一层(L-1):

           ?C/?b_j^L-1= (∑_m(?C/?a_m^L)(?a_m^L/?z_m^L)(?z_m^L/?a_j^L-1))(/?a_j^L-1/?z_j^L-1)(?z_j^L-1/?b_j^L-1)

                           = (∑_mδ_m^Lω_mj^L)σ‘(z_j^L-1)

                           = δ_j^L-1

      对于处输入层的任何一层(l)：

            ?C/?b_j^l = (?C/?z_j^l )(?z_j^l/?b_j^l) = δ_j^l