前言
前面介绍的栈、队列都是线性结构(linear structure)。而树是非线性结构(non-linear structure)。因此,树中的元素之间一般不存在类似于线性结构的一对一的关系,更多地表现为多对多的关系。直观地看,它是数据元素(在树中称为节点)按分支关系组织起来的结构。显然,树形结构是比线性结构更复杂的一种数据结构类型。
树
树是含有n个节点的有穷集合,其中有一个节点比较特殊称为根节点。在图示树时,用一条边连接两个有逻辑关系的节点,这个关系被称为父子关系。
二叉树
二叉树(Binary Tree)由节点的有限集合构成。这个集合或者为空集,或者为由一个根节点(root)和两棵互不相交,分别称为这个根的左子树(left subtree)和右子树(right subtree)的二叉树组成的集合。
一棵二叉树的示意图:
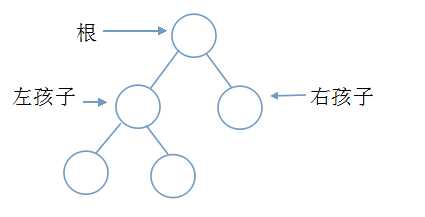
树和二叉树的主要区别
① 树中节点的最大度数没有限制,而二叉树节点的度不超过2。
② 树中节点的孩子节点,无左右之分,而二叉树中是有区分的,即孩子是有区别的:左孩子、右孩子,且次序不可颠倒。
③ 树的结点个数至少为1,而二叉树的结点个数可以为0。
常见概念
⑴ 节点的度:某节点的度定义为该节点孩子节点的个数。
⑵ 叶子节点:度为0的节点。
⑶ 树的度:一棵树中,最大的节点的度称为树的度。
⑷节点的高度:从该节点起到叶子节点的最长简单路径的边数。(简单路径:无重复边的路径)
⑸ 树的高度:根节点的高度。
⑹ 节点的层数:从根开始定义起,根为第1层,根的子节点为第2层,以此类推。
⑺ 数的层数:根节点的层数。
⑻ 节点的深度:即该节点的层数。
⑼ 树的深度:根节点的深度。
⑽ 外节点:叶子节点。
⑾ 内节点:除叶子节点之外的节点。
⑿ 满二叉树:二叉树中节点的度只能是0或2。
⒀ 完全二叉树:除最后一层,每一层的节点数都达到最大。最后一层若是没满,则节点集中在左边,空的只能是右边。
⒁ 扩充二叉树:对二叉树中度为1的节点和叶子节点添加空节点,使之成为满二叉树。
注:关于树深度、层数、高度的定义会有不同的说法:有从0开始计数的,也有从1开始计数的。从哪儿开始计数不是关键,关键在于一致性,量的写法要一致。
几个量的关系
① 对于二叉树,根节点是第一层,则第i层至多有 个结点。若共有k层,则最多有节点
个结点。若共有k层,则最多有节点 个。
个。
② 按层次顺序对一棵有n个节点的完全二叉树的所有节点从0到n-1编号。若父节点的编号是i,则左孩子的编号是2*i+1,右孩子的编号是2*i+2。(当然,这是在存在左右孩子的情况下)。同样的,若孩子(无论左右孩子)节点是i,则父节点是 (i-1)/2。
③ 对于一棵满二叉树,外部节点或者说是叶子节点数是n,则内部节点数是n-1。
④ 对于一棵二叉树,用ni表示度为i的节点个数,则n0=n2+1。证明如下:总节点数n=n0+n1+n2。用e表示边数,则n=e+1,这是因为除根节点外,每一个节点都和一条边对应。同时,e=2n2+n1,推出n0+n1+n2=2n2+n1+1,化简即得n0=n2+1。这个结论用语言表述:二叉树中,叶子节点比度为2的节点多一个。
⑤ 有n个节点的完全二叉树,树高度
⑥ 在二叉树中,第i层的第一个节点(最左边的节点)的编号是
示意图
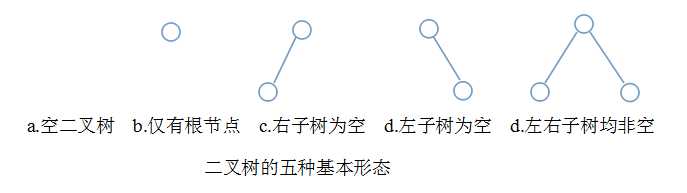
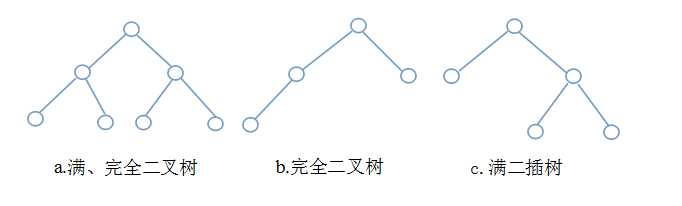
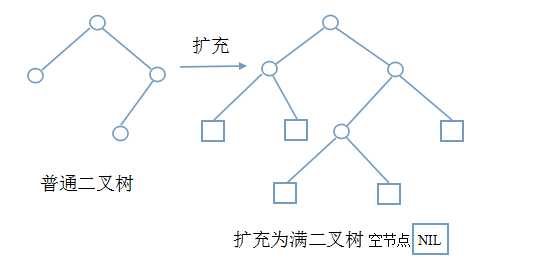
二叉树遍历
在计算机科学中,二叉树是每个节点最多有两个子树的树结构。通常子树被称作“左子树”(left subtree)和“右子树”(right subtree)。
一颗简单的二叉树示意图:
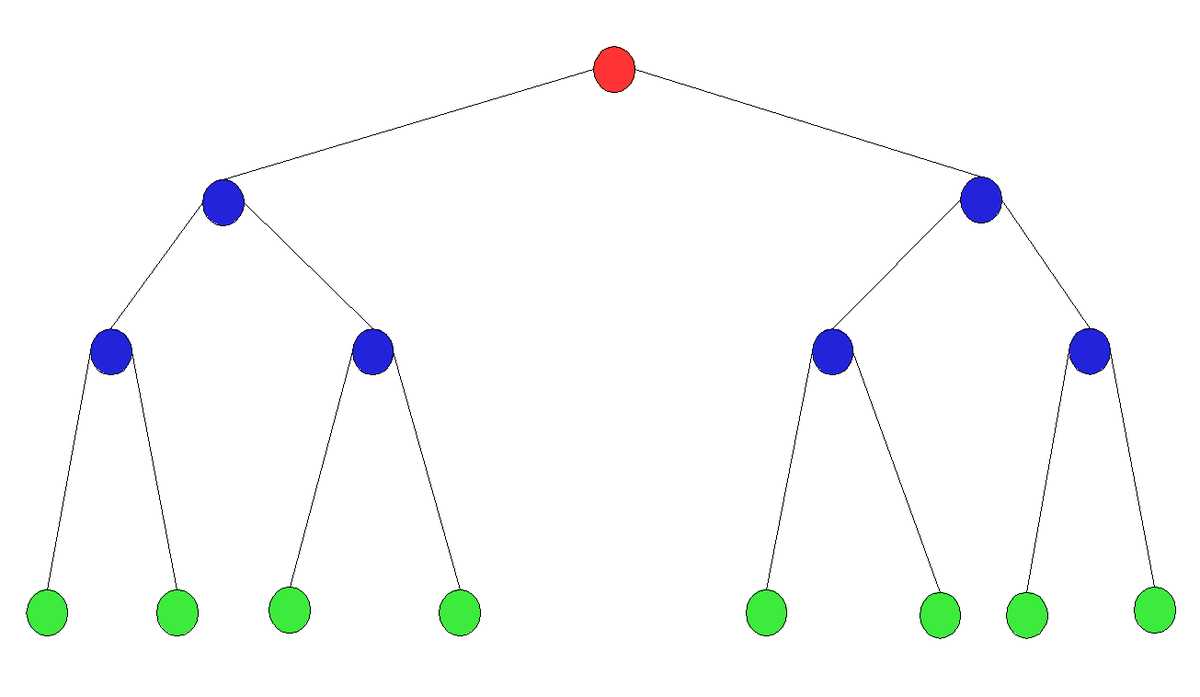
二叉树的遍历分为三种:前(先)序、中序、后序遍历。
设L、D、R分别表示二叉树的左子树、根结点和遍历右子树,则先(根)序遍历二叉树的顺序是DLR,中(根)序遍历二叉树的顺序是LDR,后(根)序遍历二叉树的顺序是LRD。(D根结点的顺序遍历从第一个到最后一个,其余LR)
还有按层遍历二叉树。这些方法的时间复杂度都是O(n),n为结点个数。
假设我们有一个包含值的value和指向两个子结点的left和right的树结点结构。我们可以写出这样的过程:
先序遍历(递归实现):
visit(node)
print node.value
if node.left != null then visit(node.left)
if node.right != null then visit(node.right)
中序遍历(递归实现):
visit(node)
if node.left != null then visit(node.left)
print node.value
if node.right != null then visit(node.right)
后序遍历(递归实现):
visit(node)
if node.left != null then visit(node.left)
if node.right != null then visit(node.right)
print node.value
二叉树创建和遍历:
public class BinaryTree
{ private Node root; //内部节点类 private class Node
{ private Node left; private Node right; private int data; public Node(int data)
{ this.left = null; this.right = null; this.data = data; } } public BinaryTree()
{ root = null; }
//递归创建二叉树 public void buildTree(Node node,int data)
{ if(root == null)
{ root = new Node(data); }
else
{ if(data < node.data)
{ if(node.left == null)
{ node.left = new Node(data); }
else
{ buildTree(node.left,data); } }
else
{ if(node.right == null)
{ node.right = new Node(data); }
else
{ buildTree(node.right,data); } } } } //前序遍历 public void preOrder(Node node)
{ if(node != null)
{ System.out.println(node.data); preOrder(node.left); preOrder(node.right); } } //中序遍历 public void inOrder(Node node)
{ if(node != null)
{ inOrder(node.left); System.out.println(node.data); inOrder(node.right); } } //后序遍历 public void postOrder(Node node)
{ if(node != null)
{ postOrder(node.left); postOrder(node.right); System.out.println(node.data); } } public static void main(String[] args)
{ int[] a = {2,4,12,45,21,6,111}; BinaryTree bTree = new BinaryTree(); for (int i = 0; i < a.length; i++)
{ bTree.buildTree(bTree.root, a[i]); } bTree.preOrder(bTree.root); bTree.inOrder(bTree.root); bTree.postOrder(bTree.root); } }
插入操作
二叉树查找树b插入操作x的过程如下:
① 若b是空树,则直接将插入的结点作为根结点插入。
② x等于b的根结点的数据的值,则直接返回,否则。
③ 若x小于b的根结点的数据的值,则将x要插入的结点的位置改变为b的左子树,否则。
④ 将x要出入的结点的位置改变为b的右子树。
public void insert(T t) { rootTree = insert(t, rootTree); } public BinaryNode insert(T t,BinaryNode node) { if(node==null) { //新构造一个二叉查找树 return new BinaryNode(t, null, null); } int result = t.compareTo(node.data); if(result<</SPAN>0) node.left= insert(t,node.left); else if(result>0) node.right= insert(t,node.right); else ;//doNothing return node; }
删除操作
对于二叉查找树的删除操作(这里根据值删除,而非结点)分三种情况:
不过在此之前,我们应该确保根据给定的值找到了要删除的结点,如若没找到该结点
不会执行删除操作!
下面三种情况假设已经找到了要删除的结点。
① 如果结点为叶子结点(没有左、右子树),此时删除该结点不会玻化树的结构
直接删除即可,并修改其父结点指向它的引用为null。如下图: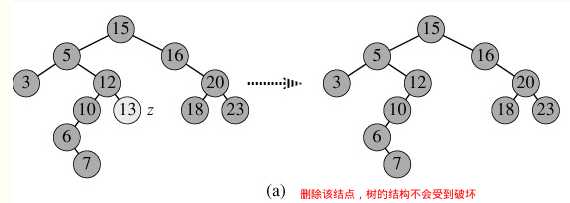
② 如果其结点只包含左子树,或者右子树的话,此时直接删除该结点,并将其左子树
或者右子树设置为其父结点的左子树或者右子树即可,此操作不会破坏树结构。
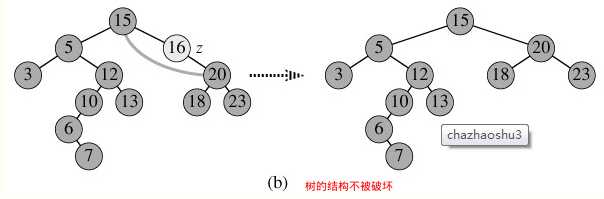
③ 当结点的左右子树都不空的时候,一般的删除策略是用其右子树的最小数据 (容易找到)代替要删除的结点数据并递归删除该结点(此时为null),因为 右子树的最小结点不可能有左孩子,所以第二次删除较为容易。 z的左子树和右子树均不空。找到z的后继y,因为y一定没有左子树,所以可以删除y,并让y的父亲节点成为y的右子树的父亲节点,并用y的值代替z的值.如图:
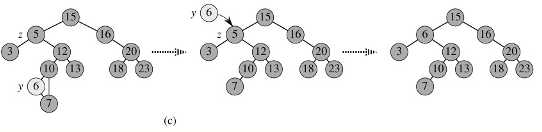
public void remove(T t) { rootTree = remove(t,rootTree); } public BinaryNode remove(T t,BinaryNode node) { if(node == null) return node;//没有找到,doNothing int result = t.compareTo(node.data); if(result>0) node.right = remove(t,node.right); else if(result<</SPAN>0) node.left = remove(t,node.left); else if(node.left!=null&&node.right!=null) { node.data = findMin(node.right).data; node.right = remove(node.data,node.right); } else node = (node.left!=null)?node.left:node.right; return node; }
查找二叉树节点
在二叉查找树中查找x的过程如下:
① 若二叉树是空树,则查找失败。
② 若x等于根结点的数据,则查找成功,否则。
③ 若x小于根结点的数据,则递归查找其左子树,否则。
④ 递归查找其右子树。
public TreeNode search(int Key) { TreeNode node = root; // 首先定义一个节点让其指向根,在下面的循环中 // 只要节点值不等于要查找的节点值就进入循环如果没有找到则返回null while (node.keyValue != Key) { if (Key < node.keyValue) { // 如果要查找的值小于节点值则指向左节点 node = node.leftNode; } else { // 否则指向右节点 node = node.rightNode; } if (node == null) { // 如果节点为空了则返回null return null; } } return node; }
最小值和最大值
思路:最大值一直往右走,最小值一直往左走。
public int max() { TreeNode node = root; TreeNode parent = null; while (node != null) { parent = node; node = node.rightNode; } return parent.keyValue; } public int min() { TreeNode node = root; TreeNode parent = null; while (node != null) { parent = node; node = node.leftNode; } return parent.keyValue; }
树的深度
int length(Node root){ int depth1; int depth2; if(root == null) return 0; //左子树的深度 depth1 = length(root.right); //右子树的深度 depth2 = length(root.left); if(depth1>depth2) return depth1+1; else return depth2+1; }
