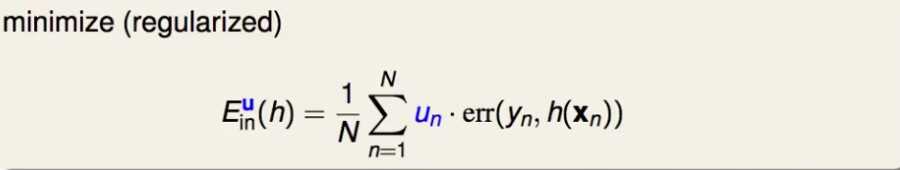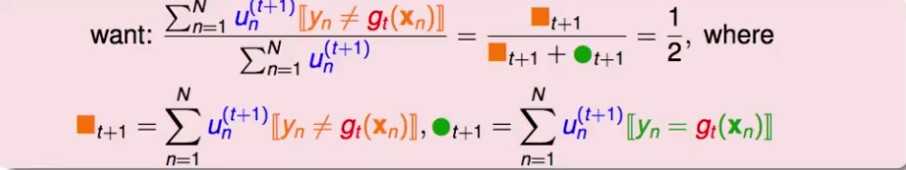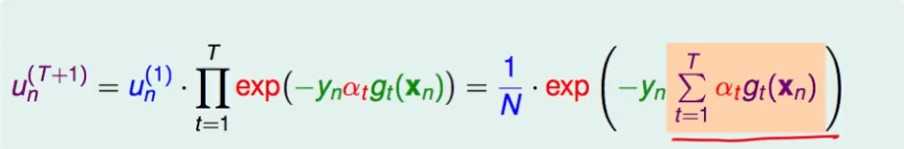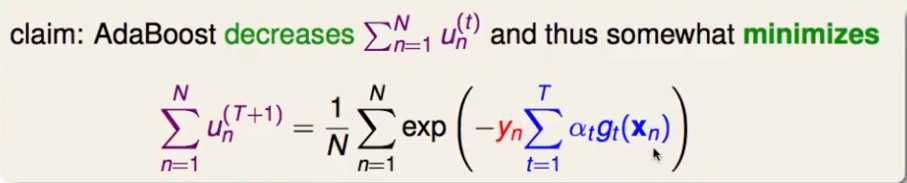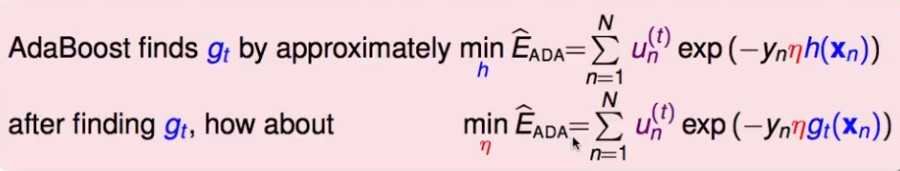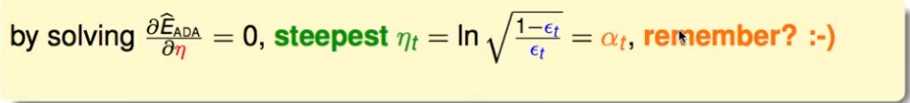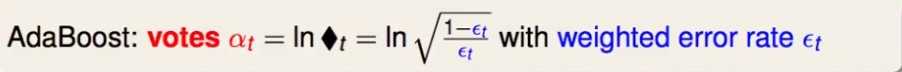Adaboost推导
每一笔样本都必须有一个权重，因此子模型要支持样本可以带权重，亦即在计算误差时可以考虑要本的权重。
例如SVM，LR中通过稍微损失函数使得可以考虑样本的权重：
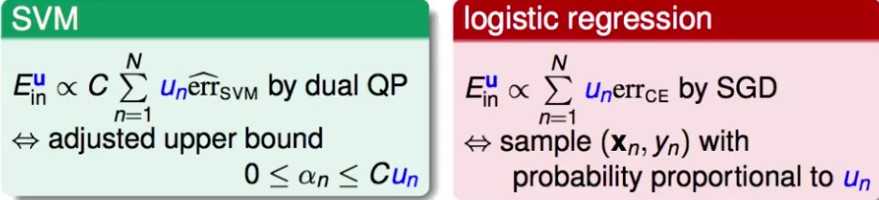
SVM（软间隔，硬间隔貌似没有损失函数）是通过在松弛项前面增加权重。相应的，推导后，alpha的上限C也要乘以权重；
LR是直接将该样本上的误差乘以损失函数。
现在假定子模型可以支持每个样本都有权重了。
子模型相差越大，最后集成时效果越好，怎样尽量得到不一样的子模型呢？
考虑两个时刻的子分类器gt,g(t+1), 它们对应的权重是ut,u(t+1).
如果gt在以u(t+1)为样本权重表现不好，那么以u(t+1)为样本权重训练得到的g(t+1)肯定和gt相差很大。
目标： 对于二元分类而言，要使gt在u(t+1)上的分类效果最差，即gt在u(t+1)上的分类效果跟瞎猜没区别，即分类正确率为0.5
即：调整u(t+1)，使gt在u(t+1)上的分类正确率为0.5
如何调整呢？将gt分类的结果分为正确分类的部分，和错误分类的部分。将这两部分的带权误差分别加起来：
那么要使正确部分和错误部分的带权误差相等
简单方法：分类正确的样本都乘以分类错误的样本的比例；分类错误的样本都乘以分类正确的样本的比例。这样刚好可以使两部分的带权误差相等。
基于上面的这种权重更新的方式，重新定义一个放缩因子t：
正确的样本需要除以t；错误的样本需要乘以t
这个放缩因子的含义：t如果大于1，表明样本的分类正确率>0.5; 因此如果此时正确样本除以t，错误样本乘以t，就真的是降低正确样本权重，提高错误样本权重。
初始的权重u0: 均分
最后如何继承所有的子模型？ 可以自行决定，但是平均相加不是最好的。
想法：表现好的子模型的权重更高
adaBoosting的选择： 子模型的权重是 ln(t)
在生成每一个子模型的时候，顺带计算其在最后集成时的权重alpha
AdaBoosting的理论保证
一个理论证明：只需要子模型的分类准确率>0.5, 就可以在log(N）轮内，让E_in = 0
理解Adaboost（Adaboost等价于以指数误差为损失函数的前向加法模型 from 李航）
所谓前向加法模型，即一个一个地添加子模型，使得最后所有子模型的加权平均结果的预测效果最好（而不是同时产生所有的子模型）
之前将adaboost, 说它将每个子模型的权重设为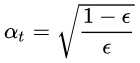
（
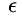是当前子模型的预测错误率）,但是对于为什么这样设定只给出了一些直观上认识，这一节换一个角度看adaboost，从理论上说明为什么要这样设定。
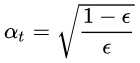（是当前子模型的预测错误率）,但是对于为什么这样设定只给出了一些直观上认识，这一节换一个角度看adaboost，从理论上说明为什么要这样设定。首先将adaboost中，正确的分类样本和错误的分类样本的权重更新公式写成统一形式：
这里用到了子模型的权重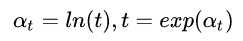
.这样ut可以写成u1再一系列连乘的结果。
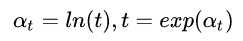.这样ut可以写成u1再一系列连乘的结果。
注意标黄的部分，其实就是到t为止前t个子模型的预测结果（都是+1或-1）的加权平均，如果再加上sign操作，就是前t个子模型集成的模型！ （后面可以看到，整个exp的式子，其实就是前t个模型的集成模型的指数误差）
称标黄的部分，即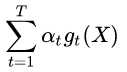
为voting score.
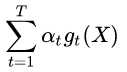为voting score.那么在adaboost中，在第t+1个子模型中样本xn的权重，实际上与前t个子模型对它的voting score是指数关系
对于adaboost而言，随着子模型的增加，预测效果应该越来越好。即如果到了第t轮，把这前t个模型的集成模型直接用来预测样本xn，那么当然是希望分类正确，并且margin越大越好
这样带来的结果就是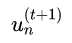
很小！ 即样本xn在第t+1个子模型上的权重很小
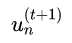很小！ 即样本xn在第t+1个子模型上的权重很小因此，下面要证明adaboost具有一个性质： 越往后的子模型，每个样本的权重越来越小（亦即所有样本的权重之和越来越小），也即下面的式子右边的部分越来越小。（后面可以看到，权重越小，代表指数误差越小）
为了证明这一点，将上面的式子的右边看成是一个损失函数，用梯度下降法来使得这个损失函数越来越小。
假设用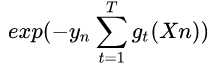
作为损失函数，用voting score来做预测（蓝色部分,s），那么随着ys的值得变化，导致的误差的变化是(假设正确的label是1)：
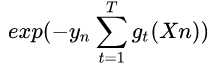作为损失函数，用voting score来做预测（蓝色部分,s），那么随着ys的值得变化，导致的误差的变化是(假设正确的label是1)：
这个误差被称为指数误差（exponential loss function)
指数误差定义：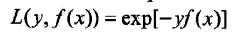
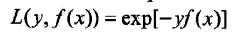
证明： adaboost 等价于 指数误差的前向加法模型
假设前面已经有了t-1个子模型，要怎么加入第t个子模型呢？考虑对指数误差进行梯度下降，找到第t个子模型h（这里是对一个模型梯度下降,即在前面的所有子模型中，加上这个子模型*步长）,将它加到前面的子模型中去做预测，使指数误差最小：
注意：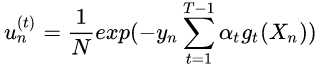 
（可见按照指数误差的定义，adaboost中样本的权重其实是前面的子模型的集成模型对它的指数误差，这也符合boosting的思想，即错误越大，权重越大）,第二步用这个替换
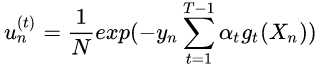（可见按照指数误差的定义，adaboost中样本的权重其实是前面的子模型的集成模型对它的指数误差，这也符合boosting的思想，即错误越大，权重越大）,第二步用这个替换
推导的最后一步是对exp函数在原点附近进行泰勒展开
因此，需要最小化这一项：
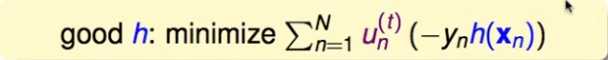
这一项只用考虑子模型h的分类是否正确，同时每个样本都以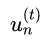
为权重。（这不刚好使以
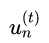为权重去训练一个子模型么）
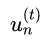为权重。（这不刚好使以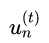为权重去训练一个子模型么
因此只需要使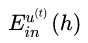
更小即可，
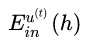表示第t个子模型h的，以
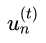为样本权重的分类错误率。而adaboost刚好是以
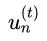为样本权重去训练下一个子模型，即每个子模型在以
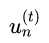为权重训练时就刚好使
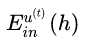最小。
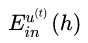更小即可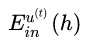，表示第t个子模型h的，以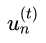为样本权重的分类错误率。而adaboost刚好是以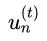为样本权重去训练下一个子模型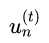，为权重训练时就刚好使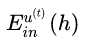最小。因此，整个adaboost的过程，刚好使这个指数误差越来越小！
刚才找出了最小化指数误差，下一个子模型应该是什么样的。但是在梯度下降了还有一个步长：
考虑寻找步长，使误差函数下降的最多（steepest descent）：
对于第t个子模型，根据其分类正确还是分类错误，考虑对误差函数的值的影响：
带权分类错误的样本数目为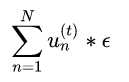
,带权分类正确的样本数目为
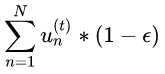，这样就可以得到上面的最后一项。
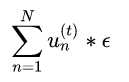,带权分类正确的样本数目为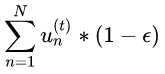，这样就可以得到上面的最后一项。考虑寻找最佳的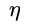
，使上式最小，对其求导=0， 刚好得到：
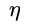，使上式最小，对其求导=0， 刚好得到：
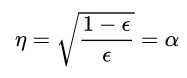,即之前adaboost中定义的结果。AdaBoost Decision Tree
考虑将决策树应用于Adaboost, 如何更改样本的权重？
因为决策树本身不支持样本有权重，因此可以将样本的权重当做这个样本被抽样到的概率，这样按照每个样本的权重抽样后得到的数据集可以大致反映每个样本的权重。而不再采用随机抽样。
考虑adaboost如何给每个子模型分配权重：
即：分类正确率越高的子模型，最后的权重越大。
但是，如果是决策树运用于Adaboost，由于决策树在完全生长的情况下E_in=0,因此它的权重会无限大！
因此，需要对决策树进行剪枝，同时不能让这个决策树的样本包含所有的样本（这个在上面的根据权重的抽样方式已经解决了）
这就是AdaBoost Decision Tree的通常做法
