一、什么是Catalan数
说到Catalan数,就不得不提及Catalan序列,Catalan序列是一个整数序列,其通项公式是

递推公式是
C(n) = C(1)*C(n-1) + C(2)*C(n-2) + ... + C(n-1)C(1),n>=2
我们从中取出的 就叫做第n个Catalan数,前几个Catalan数如下:
就叫做第n个Catalan数,前几个Catalan数如下:
1, 1, 2, 5, 14, 42, 132, 429, 1430, 4862, 16796, 58786, 208012, 742900, 2674440, 9694845, 35357670, …
咋看之下没什么特别的,但是Catalan数却是许多计数问题的最终形式。
二、Catalan数在组合计算中的应用
1、矩阵链乘: P=a1×a2×a3×……×an,依据乘法结合律,不改变其顺序,只用括号表示成对的乘积,有几种括号化的方案?
2、一个栈(无穷大)的进栈序列为1,2,3,…,n,有多少个不同的出栈序列?
3、n个节点构成的二叉树,共有多少种情形?
4、求一个凸多边形区域划分成三角形区域的方法数?
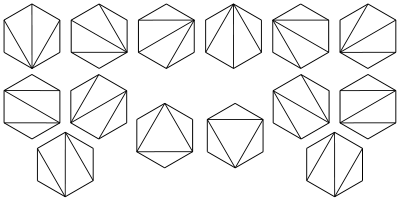
5、在圆上选择2n个点,将这些点成对链接起来使得所得到的n条线段不相交,一共有多少种方法?(下图供参考)
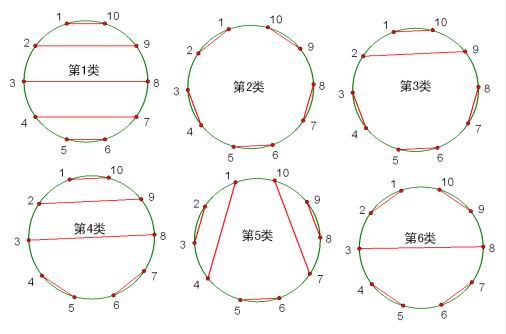
6、n*n的方格地图中,从一个角到另外一个角,不跨越对角线的路径数为h(n).例如, 4×4方格地图中的路径有:
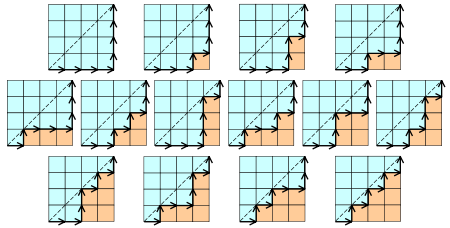
7、n层的阶梯切割为n个矩形的切法数也是 。如下图所示:
。如下图所示:

8、有2n个人排成一行进入剧场。入场费5元。其中只有n个人有一张5元钞票,另外n人只有10元钞票,剧院无其它钞票,问有多少中方法使得只要有10元的人买票,售票处就有5元的钞票找零?
9、甲乙两人比赛乒乓球,最后结果为20∶20,问比赛过程中甲始终领先乙的计分情形的种数。
10、2n个高矮不同的人,排成两排,每排必须是从矮到高排列,而且第二排比对应的第一排的人高,问排列方式有多少种?
一,问题描述
给定一个以字符串形式表示的入栈序列,请求出一共有多少种可能的出栈顺序?如何输出所有可能的出栈序列?
比如入栈序列为:1 2 3 ,则出栈序列一共有五种,分别如下:1 2 3、1 3 2、2 1 3、2 3 1、3 2 1
二,问题分析
先介绍几个规律:
①对于出栈序列中的每一个数字,在它后面的、比它小的所有数字,一定是按递减顺序排列的。
比如入栈顺序为:1 2 3 4。
出栈顺序:4 3 2 1是合法的,对于数字 4 而言,比它小的后面的数字是:3 2 1,且这个顺序是递减顺序。同样地,对于数字 3 而言,比它小的后面的数字是: 2 1,且这个顺序是递减的。....
出栈顺序:1 2 3 4 也是合法的,对于数字 1 而言,它后面没有比它更小的数字。同样地,对于数字 2 而言,它后面也没有比它更小的数字。
出栈顺序:3 2 4 1 也是合法的,对于数字 3 而言,它后面比 3 小的数字有: 2 1,这个顺序是递减的;对于数字 2 而言,它后面的比它 小的数字只有 1,也算符合递减顺序;对于数字 4 而言,它后面的比它小的数字也只有1,因此也符合递减顺序。
出栈顺序:3 1 4 2 是不合法的,因为对于数字 3 而言,在3后面的比3小的数字有:1 2,这个顺序是一个递增的顺序(1-->2)。
因此,当给定一个序列时,通过这个规律 可以轻松地判断 哪些序列是合法的,哪些序列是非法的。
②给定一个入栈顺序:1 2 3 .... n,一共有多少种合法的出栈顺序?参考:百度百科卡特兰数
答案是 卡特兰数。即一共有:h(n)=c(2n,n)/(n+1) 种合法的出栈顺序。
如果仅仅只需要求出一共有多少种合法的出栈顺序,其实就是求出组合 C(2n,n)就可以了。而求解C(2n,n),则可以用动态规划来求解,具体可参考: 排列与组合的一些定理
三,代码实现
给定一个入栈顺序,比如 1 2 3 ,如何输出所有可能的出栈顺序?
思路①:先求出入栈顺序的所有排列(即全排列),并将排列保存到一个LinkedList<String>中,然后依次遍历每一个序列,判断该序列是否是合法的序列。
所谓合法的序列,就是满足上面的规律1:对于出栈序列中的每一个数字,在它后面的、比它小的所有数字,一定是按递减顺序排列的。 关于如何求解一个序列的全排列,可参考:JAVA求解全排列
完整代码实现如下:(实现得不好,感觉比较复杂)

import java.util.Collections;
import java.util.Iterator;
import java.util.LinkedList;
public class AllStackPopOrder {
public static LinkedList<String> allPermutation(String str){
if(str == null || str.length() == 0)
return null;
//保存所有的全排列
LinkedList<String> listStr = new LinkedList<String>();
allPermutation(str.toCharArray(), listStr, 0);
//print(listStr);//打印全排列
return listStr;
}
private static void allPermutation(char[] c, LinkedList<String> listStr, int start){
if(start == c.length-1)
listStr.add(String.valueOf(c));
else{
for(int i = start; i <= c.length-1; i++)
{
//只有当没有重叠的字符 才交换
if(!isSwap(c, start, i))
{
swap(c, i, start);//相当于: 固定第 i 个字符
allPermutation(c, listStr, start+1);//求出这种情形下的所有排列
swap(c, start, i);//复位
}
}
}
}
private static void swap(char[] c, int i, int j){
char tmp;
tmp = c[i];
c[i] = c[j];
c[j] = tmp;
}
private static void print(LinkedList<String> listStr)
{
Collections.sort(listStr);//使字符串按照‘字典顺序‘输出
for (String str : listStr) {
System.out.println(str);
}
System.out.println("size:" + listStr.size());
}
//[start,end) 中是否有与 c[end] 相同的字符
private static boolean isSwap(char[] c, int start, int end)
{
for(int i = start; i < end; i++)
{
if(c[i] == c[end])
return true;
}
return false;
}
public static LinkedList<String> legalSequence(LinkedList<String> listStr){
Iterator<String> it = listStr.iterator();
String currentStr;
while(it.hasNext())//检查全排列中的每个序列
{
currentStr = it.next();
if(!check(currentStr))
it.remove();//删除不符合的出栈规律的序列
}
return listStr;
}
//检查出栈序列 str 是否 是合法的出栈 序列
private static boolean check(String str){
boolean result = true;
char[] c = str.toCharArray();
char first;//当前数字.
int k = 0;//记录 compare 数组中的元素个数
char[] compare = new char[str.length()];
for(int i = 0; i < c.length; i++)
{
first = c[i];
//找出在 first 之后的,并且比 first 小的数字
for(int j = i+1; j < c.length; j++)
{
if(c[j] > first)
continue;
else
{
compare[k++] = c[j];//将比当前数字小的 所有数字 放在compare数组中
}
}
if(k == 0)
continue;
else{
for(int m = 0; m < k-1; m++)//判断 compare 数组是否是 递减的顺序
{
if(compare[m] < compare[m+1])
{
result = false;//不符合递减顺序
return result;
}
}
}
k=0;
}
return result;
}
//hapjin test
public static void main(String[] args) {
String str = "1234";
LinkedList<String> listStr = legalSequence(allPermutation(str));
print(listStr);
}
}
思路②:直接求出合法的出栈序列。【而不是像思路①那样:先求出所有可能的出栈序列(求全排列),然后再找出合法的出栈序列。】
待完成。
参考
百度百科:https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0/6125746?fr=aladdin

