题目描述
设d(x)为x的约数个数,给定N、M,求 \sum^N_{i=1}\sum^M_{j=1}d(ij)∑i=1N?∑j=1M?d(ij)
输入输出格式
输入格式:
输入文件包含多组测试数据。第一行,一个整数T,表示测试数据的组数。接下来的T行,每行两个整数N、M。
输出格式:
T行,每行一个整数,表示你所求的答案。
输入输出样例
说明
1<=N, M<=50000
1<=T<=50000
有一个定理
$d\left( i,j\right) =\sum _{x|i}\sum _{y|j}\left[ \gcd \left( x,y\right) = 1\right]$
然后大力推公式就好了
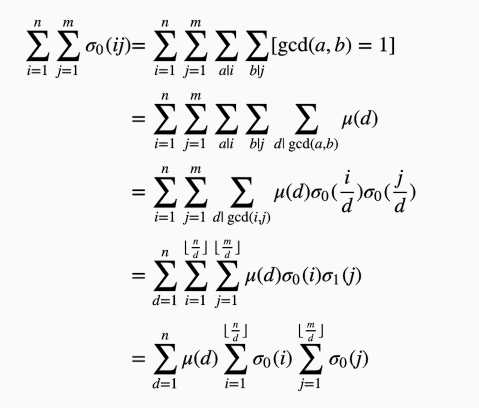
后面两项暴力分块预处理
// luogu-judger-enable-o2 #include<cstdio> #include<cstring> #include<cmath> #include<algorithm> using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();} return x*f; } int N,M; int vis[MAXN],prime[MAXN],tot=0,mu[MAXN]; long long divv[MAXN]; void GetMu() { vis[1]=1;mu[1]=1; for(int i=2;i<=N;i++) { if(vis[i]==0) prime[++tot]=i,mu[i]=-1; for(int j=1;j<=tot&&i*prime[j]<=N;j++) { vis[i*prime[j]]=1; if(i%prime[j]==0){mu[i*prime[j]]=0;break;} else mu[i*prime[j]]=-mu[i]; } } for(int i=1;i<=N;i++) mu[i]+=mu[i-1]; for(int i=1;i<=N;i++) for(int j=1,nxt;j<=i;j=nxt+1) nxt=i/(i/j), divv[i]+=(long long )(nxt-j+1)*(i/j); } main() { #ifdef WIN32 freopen("a.in","r",stdin); #else // freopen("SDOI2015yue.in","r",stdin); // freopen("SDOI2015yue.out","w",stdout); #endif N=50000; GetMu(); int QWQ=read(); while(QWQ--) { long long ans=0; N=read(),M=read(); if(N>M) swap(N,M); for(int i=1,nxt;i<=N;i=nxt+1) { nxt=min(N/(N/i),M/(M/i)); ans+=(long long )(mu[nxt]-mu[i-1])*divv[N/i]*divv[M/i]; } printf("%lld\n",ans); } return 0; }
