题目传送门
通往Codeforces的航线
通往vjudge的航线
题目大意
给定一个仅包含小写字母的串$s$,要求插入恰好$n$个小写字母字符,使得新串为回文串。问这样得到的新串有多少个是本质不同回文串。
$1\leqslant |s| \leqslant 200,1 \leqslant n \leqslant 10^{9} $
神题orz...orz...orz。Petr orz...orz...orz。
好了开始扯正题了。
任意位置插入并不太好处理。可以转化一下这个问题,求一个长度为$|s| + n$的回文串,要求以$|s|$作为其中的一个子序列。
因为是回文串,所以可以从两边开始向中间动态规划,用$f[i][l][r]$表示我已经在半边加入了$i$个字符,中间还需要存在一个子序列是$s$的$[l, r]$这一段。
转移枚举是否是$s_{l}$或者$s_{r}$的字符,如果两端相等需要特判。
然而这样转移$O(|s|^{2}n)$,可以用矩阵快速幂优化成$O(|s|^{6}\log n)$。非常优秀,完美TLE。
考虑这么转移的一个过程可以看做一个自动机:
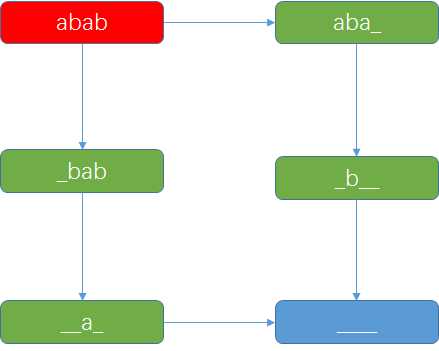
其中红色的节点有24个自环转移(自己到自己),绿色节点有25个自环转移,蓝色节点为终止状态,有26个自环转移。
原问题可以看成从起始状态$[1, |s|]$,通过$n$次转移到终止状态的方案数。
然而这有什么用呢?
现在将计数的过程分成两个步骤:
step 1
现在不考虑自环转移。对于每走一条红色状态的向外转移边意味着未匹配的序列长度减一(转移到$[l + 1, r]$或$[l, r - 1]$)。每走一条绿色状态的向外转移边意味着序列长度减少2,除了形如$[i, i]$的状态。但是由于它的例外很特殊,所以当我们确定路经红色状态的向外转移边的个数$n24$,那么就有唯一确定的路经绿色状态的向外转移边的个数$n25$与之对应,它的个数为$n25 = \left \lceil \frac{|s| - n24}{2} \right \rceil$。
用$f[l][r][k]$表示当前状态为$[l, r]$,已经走过的红色状态的向外转移边的个数为$k$的方案数。现在约定用$[0, 0]$表示终止状态。
这个动态规划可以在$O(|s|^{3})$内完成,这就是第一部分的计数。
step 2
现在考虑将自环转移插入路径中。
考虑在路径中插入自环转移,使得路径长度达到要求。
显然,插入自环转移的方案数之和红色状态、绿色状态以及终止状态的个数有关而与它们的排列顺序无关。
因为对于两个满足上面三个状态数相同但不同的简单路径,显然无论我们怎么插入自环最终都对应不同的回文串。另外我们可以对它们的节点建立一一映射。这样就能证明上面这条优美的性质。然而这样有什么用呢?
考虑将红色状态扔到左边,绿色状态扔到右边,每个绿色状态接一个终止状态(注意,每一个都需要一个不同的终止状态)

如果红色状态足够多,绿色状态也足够多,那么对于每一条无标号有状态类型的路径都可以对应到这样的一个自动机上从某个节点开始,到达终止状态的路径。
由于红色状态至多$|s| - 1$个(因为最后一个状态一定有25个自环转移),绿色状态至多$\left \lceil \frac{|s|}{2} \right \rceil$个,终止状态与绿色状态数量相同。因此总状态数是$O(|s|)$的,因此,我们可以在$O(|s|^{3}\log n)$的时间内解决这个问题。
结束了吗?
当然没有!让我们来随手打一组数据:
aa 1
期望26,读到51。
为什么会这样?让我们来回顾一下,在考虑特殊的绿色状态的转移时,我们让它"自适应"是加入1个字符还是2个。但是在状态$[l, l + 1]$,且满足$s_{l} = s_{r}$时,如果转移到终止状态,那么强制使得串长增加了2。如果$|s| + n$是奇数,且最后一个走过的节点是长度为2的绿色状态,那么这样会使得最终的串长为偶数。现在考虑将它从答案中减去。如何避免这样的情况?让最后一个走过的节点没有这样的强制限制就好了。但是除了长度为2的绿色状态这样的限制,其他状态都有"自适应"的能力,因此我们只需要减去在$|s| + \left \lceil \frac{n}{2} \right \rceil - 1$步在最后一个长度为2的绿色状态的方案数就好了。
因为我们枚举$n24$,所以另外$n25 = \left \lceil \frac{|s| - n24}{2} \right \rceil$,所以,可以根据$|s| - n24$的奇偶性来判断最后一个绿色状态的长度。
这样就解决这个问题。然后还有一点想瞎扯一下。这算法的本质是先进行带标号的计数,然后再进行无标号的计数,最后再进行标号。
当然还有一些神奇的解法,可以跑得贼快,只是我不会。打上Lazy Tag,以后再来学吧。
另外,如果代码比较丑,请卡常数。一个不错的卡常数的方法利用转移矩阵是优美的上三角。矩阵乘法的时候可以将常数减小到原来的六分之一。
Code
1 /** 2 * Codeforces 3 * Problem#506E 4 * Accepted 5 * Time: 2355ms 6 * Memory: 44928k 7 */ 8 #include <bits/stdc++.h> 9 using namespace std; 10 typedef bool boolean; 11 12 const int N = 205, M = 10007; 13 14 typedef class Matrix { 15 public: 16 int a[N << 1][N << 1]; 17 18 Matrix() { } 19 Matrix(int n) { 20 for (int i = 0; i < n; i++) 21 for (int j = 0; j < n; j++) 22 a[i][j] = ((i == j) ? (1) : (0)); 23 } 24 25 int* operator [] (int p) { 26 return a[p]; 27 } 28 29 void debug() { 30 for (int i = 0; i < 11; i++, cerr << endl) 31 for (int j = 0; j < 11; j++) 32 cerr << a[i][j] << " "; 33 } 34 }Matrix; 35 36 char str[N]; 37 int n, m, es, l; 38 int f[N][N][N]; 39 40 inline void init() { 41 scanf("%s%d", str + 1, &m); 42 n = strlen(str + 1); 43 } 44 45 void modplus(int& a, int b) { 46 a += b; 47 if (a < 0) a += M; 48 if (a >= M) a -= M; 49 } 50 51 inline void dp() { 52 f[1][n][0] = 1; 53 for (int l = n - 1; ~l; l--) { 54 for (int i = 1, j; (j = i + l) <= n; i++) { 55 for (int k = 0; k <= n; k++) { 56 if (!f[i][j][k]) continue; 57 if (str[i] == str[j]) { 58 if (i + 1 == j || i == j) 59 modplus(f[0][0][k], f[i][j][k]); 60 else 61 modplus(f[i + 1][j - 1][k], f[i][j][k]); 62 } else { 63 modplus(f[i + 1][j][k + 1], f[i][j][k]); 64 modplus(f[i][j - 1][k + 1], f[i][j][k]); 65 } 66 } 67 } 68 } 69 /* 70 for (int i = 0; i <= n; i++) 71 cerr << "0 0 " << i << " " << f[0][0][i] << endl; 72 for (int i = 1; i <= n; i++) 73 for (int j = i; j <= n; j++) 74 for (int k = 0; k <= n; k++) 75 cerr << i << " " << j << " " << k << " " << f[i][j][k] << endl; 76 */ 77 } 78 79 Matrix operator * (Matrix a, Matrix b) { 80 Matrix rt; 81 for (int i = 0; i < es; i++) 82 for (int j = i; j < es; j++) { 83 rt[i][j] = 0; 84 for (int k = i; k <= j; k++) 85 rt[i][j] = (rt[i][j] + a[i][k] * b[k][j]) % M; 86 } 87 return rt; 88 } 89 90 Matrix qpow(Matrix& a, int pos) { 91 Matrix pa = a, rt = Matrix(es); 92 for ( ; pos; pos >>= 1, pa = pa * pa) 93 if (pos & 1) 94 rt = rt * pa; 95 return rt; 96 } 97 98 Matrix g, tem, bas; 99 inline void solve() { 100 int N24 = n - 1, N25 = (n + 1) >> 1, N26 = N25; 101 es = N24 + N25 + N26, l = (m + n + 1) >> 1; 102 for (int i = 0; i < N24; i++) 103 g[i][i + 1] = 1, g[i][i] = 24; 104 for (int i = N24; i < N24 + N25; i++) { 105 g[i][i + N25] = 1, g[i][i] = 25; 106 if (i < N24 + N25 - 1) 107 g[i][i + 1] = 1; 108 } 109 for (int i = N24 + N25; i < es; i++) 110 g[i][i] = 26; 111 112 bas = g; 113 114 tem = g = qpow(bas, l - 1); 115 // g.debug(); 116 // cerr << "hahaha" << endl; 117 118 g = g * bas; 119 120 // g.debug(); 121 122 int res = 0; 123 boolean aflag; 124 for (int i = 0, n25, c; i <= N24; i++) { 125 n25 = (n - i + 1) >> 1, aflag = !((n - i) & 1); 126 c = f[0][0][i]; 127 res = (res + c * g[N24 - i][N24 + N25 + n25 - 1]) % M; 128 if (((n + m) & 1) && aflag) 129 res = (res - (c * tem[N24 - i][N24 + n25 - 1]) % M + M) % M; 130 } 131 132 printf("%d\n", res); 133 } 134 135 int main() { 136 init(); 137 dp(); 138 solve(); 139 return 0; 140 }
