本文是对 LeetCode Count Primes 解法的探讨。
题目:
Count the number of prime numbers less than a non-negative number, n.
尽管题目并没有要我们写一个最优的算法,但是身为一个程序员,优化应该是一种习惯,在编程的过程中,随着思考进行优化。只要求我们满足给定的时间和空间即可。
如果你只能想出一个最简单的方法,难道你会有什么竞争力吗?
穷举
最开始我用的就是这个方法,可以说这是最简单的一种方法了,而且最开始,我就是想的这种方法,说明:我没有对这个问题进行思考,没有去优化它,而作为一个程序员,如何提高效率是拿到一个问题首先要思考的事情。
public int countPrimes(int n) {
int num = 0;
for (int i = 2; i < n; i++) {
boolean flag = true;
for (int j = 2; j < i - 1; j++)
if (i % j == 0) {
flag = false;
break;
}
if (flag) {
num++;
}
}
return num;
}测试代码:
public static void main(String[] args) {
//获取开始时
long startTime = System.currentTimeMillis();
System.out.println("The num is " + new L_204_Count_Primes().countPrimes(2000000));
long endTime = System.currentTimeMillis();
//获取结束时间
System.out.println("程序运行时间: " + (endTime - startTime) + "ms");
}时间太长,已经不能计算。
只能是奇数且小于\(\sqrt{n}\)
思考后发现
- 素数一定是奇数
- 若 n=ab 是个合数(其中 a 与 b ≠ 1), 则其中一个约数 a 或 b 必定至大为 \(\sqrt{n}\).
public int countPrimes2(int n) {
int num = 1;
for (int i = 3; i < n; i += 2) {
boolean flag = true;
for (int j = 2; j <= (int) Math.sqrt(i); j++)
if (i % j == 0) {
flag = false;
break;
}
if (flag) {
num++;
}
}
return num;
}The num is 148933
程序运行时间: 1124ms
试除法:数学知识的运用
查阅 算术基本定理可知:
算术基本定理 :
每个大于1的整数均可写成一个以上的素数之乘积,且除了质约数的排序不同外是唯一的
也就是说我们可以每个数来除以得到的素数,这样可大大减少运行次数。
public int countPrimes3(int n) {
if (n < 3) {
return 0;
}
//0 1 不算做素数,2一定是素数
List<Integer> list = new ArrayList<>();
list.add(2);
boolean flag;
for (int i = 3; i < n; i += 2) {
flag = true;
for (int j = 0; j < list.size() && list.get(j) <= (int) Math.sqrt(n); j++) {
if (i % list.get(j) == 0) {
flag = false;
break;
}
}
if (flag) {
list.add(i);
}
}
return list.size();
}The num is 148933
程序运行时间: 383ms
筛选法
埃拉托斯特尼筛法,简称埃氏筛,也有人称素数筛。这是一种简单且历史悠久的筛法,用来找出一定范围内所有的素数。
所使用的原理是从2开始,将每个素数的各个倍数,标记成合数。一个素数的各个倍数,是一个差为此素数本身的等差数列。此为这个筛法和试除法不同的关键之处,后者是以素数来测试每个待测数能否被整除。
筛选法的策略是将素数的倍数全部筛掉,剩下的就是素数了,下图很生动的体现了筛选的过程:
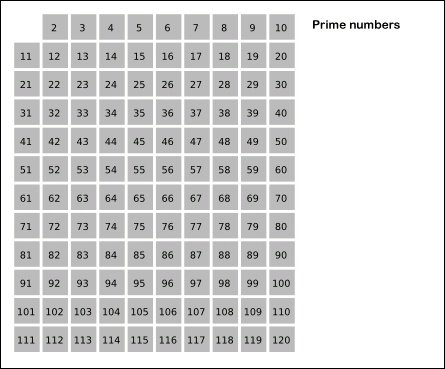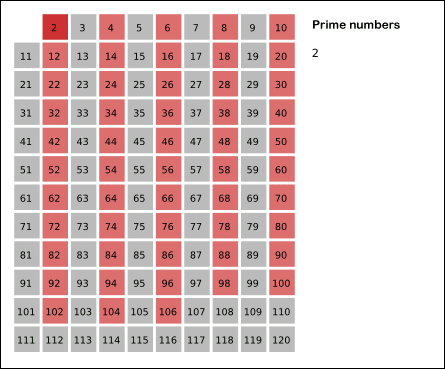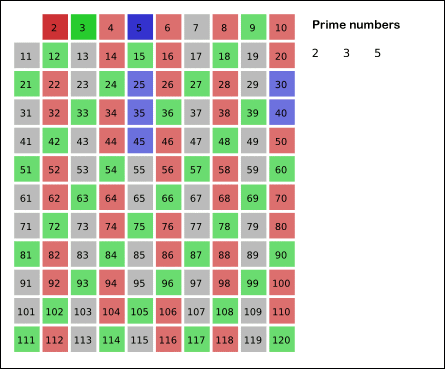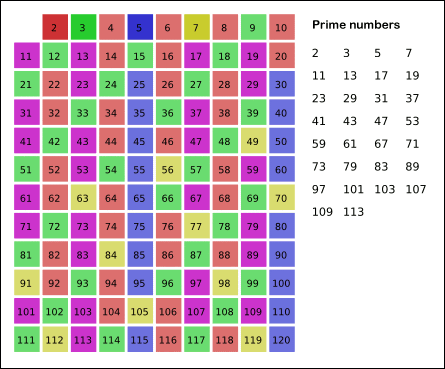
筛选的过程是先筛掉非素数,针对本文的题目,每筛掉一个,素数数量-1即可,上面说过素数的一个特点,除了2,其它的素数都是奇数,所以我们只需在奇数范围内筛选就可以了。
public int countPrimes4(int n) {
if (n < 3) {
return 0;
}
//false代表素数,true代表非素数
boolean[] flags = new boolean[n];
//0不是素数
flags[0] = true;
//1不是素数
flags[1] = true;
int num = n - 2;
for (int i = 2; i <= (int) Math.sqrt(n); i++) {
//当i为素数时,i的所有倍数都不是素数
if (!flags[i]) {
for (int j = 2 * i; j < n; j += i) {
if (!flags[j]) {
flags[j] = true;
num--;
}
}
}
}
return num;
}The num is 148933
程序运行时间: 43ms
全部代码放在:
https://github.com/morethink/algorithm/blob/master/src/algorithm/leetcode/L_204_Count_Primes.java
参考文档:
