题目描述
春春幼儿园举办了一年一度的“积木大赛”。今年比赛的内容是搭建一座宽度为n的大厦,大厦可以看成由n块宽度为1的积木组成,第i块积木的最终高度需要是hi。
在搭建开始之前,没有任何积木(可以看成n块高度为 0 的积木)。接下来每次操作,小朋友们可以选择一段连续区间[l, r],然后将第第 L 块到第 R 块之间(含第 L 块和第 R 块)所有积木的高度分别增加1。
小 M 是个聪明的小朋友,她很快想出了建造大厦的最佳策略,使得建造所需的操作次数最少。但她不是一个勤于动手的孩子,所以想请你帮忙实现这个策略,并求出最少的操作次数。
输入输出格式
输入格式:
输入文件为 block.in
输入包含两行,第一行包含一个整数n,表示大厦的宽度。
第二行包含n个整数,第i个整数为hi 。
输出格式:
输出文件为 block.out
仅一行,即建造所需的最少操作数。
输入输出样例
说明
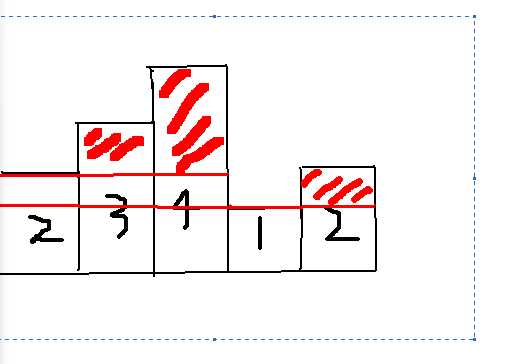
【样例解释】
其中一种可行的最佳方案,依次选择
[1,5] [1,3] [2,3] [3,3] [5,5]
【数据范围】
对于 30%的数据,有1 ≤ n ≤ 10;
对于 70%的数据,有1 ≤ n ≤ 1000;
对于 100%的数据,有1 ≤ n ≤ 100000,0 ≤ hi≤ 10000。
【题解】
显然对于每一次当遇到$h[i-1]>h[i]$的时候h[i]一定被$i-1$之前格子给覆盖了
当遇到$h[i-1]<h[i]$显然$i-1$作为一个屏障使得$i$的高度最大为h[i-1]
所以加上即为答案
#include<cstdio> int n,h[100010],t[100010],ans=0; int main() { scanf("%d",&n); for(int i=1; i<=n; i++) scanf("%d",&h[i]); for(int i=1; i<=n; i++) if(h[i-1]<h[i])ans+=h[i]-h[i-1]; printf("%d\n",ans); return 0; }
