题目描述
深海资源考察探险队的潜艇将到达深海的海底进行科学考察。
潜艇内有多个深海机器人。潜艇到达深海海底后,深海机器人将离开潜艇向预定目标移动。
深海机器人在移动中还必须沿途采集海底生物标本。沿途生物标本由最先遇到它的深海机器人完成采集。
每条预定路径上的生物标本的价值是已知的,而且生物标本只能被采集一次。
本题限定深海机器人只能从其出发位置沿着向北或向东的方向移动,而且多个深海机器人可以在同一时间占据同一位置。
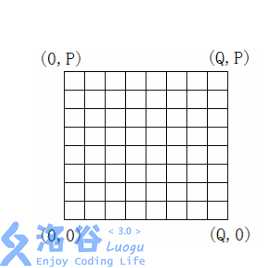
用一个 P\times QP×Q 网格表示深海机器人的可移动位置。西南角的坐标为 (0,0)(0,0) ,东北角的坐标为 (Q,P)(Q,P) 。
给定每个深海机器人的出发位置和目标位置,以及每条网格边上生物标本的价值。
计算深海机器人的最优移动方案, 使深海机器人到达目的地后,采集到的生物标本的总价值最高。
输入输出格式
输入格式:
文件的第 11 行为深海机器人的出发位置数 aa ,和目的地数 bb 。
第 22 行为 PP 和 QQ 的值。
接下来的 P+1P+1 行,每行有 QQ 个正整数,表示向东移动路径上生物标本的价值,行数据依从南到北方向排列。
再接下来的 Q+1Q+1 行,每行有 PP 个正整数,表示向北移动路径上生物标本的价值,行数据依从西到东方向排列。
接下来的 aa 行,每行有 33 个正整数 k,x,yk,x,y ,表示有 kk 个深海机器人从 (x,y)(x,y) 位置坐标出发。
再接下来的 bb 行,每行有 33 个正整数 r,x,yr,x,y ,表示有 rr 个深海机器人可选择 (x,y)(x,y) 位置坐标作为目的地。
a行和b行输入时横纵坐标要反过来
输出格式:
输出采集到的生物标本的最高总价值.
输入输出样例
说明
1\leq P,Q\leq151≤P,Q≤15
1\leq a\leq 41≤a≤4
1\leq b\leq 61≤b≤6
费用流应该比较显然
就是读入比较坑爹
需要把整张图反过来
从S向每个机器人开始的地方连容量为机器人数量,费用为0的边
从每个机器人向T连容量为数量,费用为0的边
相邻格子之间连一条容量为INF,费用为0的边,再连一条容量为1,费用为读入的边
#include<cstdio> #include<cstring> #include<queue> #include<algorithm> #define AddEdge(x,y,z,f) add_edge(x,y,z,f),add_edge(y,x,-z,0) using namespace std; const int INF=1e8+10; const int MAXN=1001+10; int N,M,S,T; int C[MAXN][MAXN]; struct node { int u,v,w,f,nxt; }edge[MAXN]; int head[MAXN],num=2; inline void add_edge(int x,int y,int z,int f) { edge[num].u=x; edge[num].v=y; edge[num].w=z; edge[num].f=f; edge[num].nxt=head[x]; head[x]=num++; } int dis[MAXN],vis[MAXN],Pre[MAXN]; bool SPFA() { memset(dis,0xf,sizeof(dis)); memset(vis,0,sizeof(vis)); queue<int>q; q.push(S); dis[S]=0; while(q.size()!=0) { int p=q.front();q.pop(); vis[p]=0; for(int i=head[p];i!=-1;i=edge[i].nxt) { if(edge[i].f&&dis[edge[i].v]>dis[p]+edge[i].w) { dis[edge[i].v]=dis[p]+edge[i].w; Pre[edge[i].v]=i; if(!vis[edge[i].v]) vis[edge[i].v]=1,q.push(edge[i].v); } } } return dis[T]<INF; } int F() { int nowflow=INF; for(int now=T;now!=S;now=edge[Pre[now]].u) nowflow=min(nowflow,edge[Pre[now]].f); for(int now=T;now!=S;now=edge[Pre[now]].u) edge[Pre[now]].f-=nowflow, edge[Pre[now]^1].f+=nowflow; return nowflow*dis[T]; } void MCMF() { int ans=0; while(SPFA()) ans+=F(); printf("%d\n",abs(ans)); } int belong[MAXN][MAXN]; int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif memset(head,-1,sizeof(head)); int a,b,P,Q; scanf("%d%d",&a,&b); scanf("%d%d",&P,&Q); P++;Q++; S=437,T=438; for(int i=1;i<=P;i++) for(int j=1;j<=Q;j++) belong[i][j]=(i-1)*Q+j; for(int i=1;i<=P;i++) { for(int j=1;j<=Q-1;j++) { int x; scanf("%d",&x); AddEdge(belong[i][j],belong[i][j+1],-x,1); AddEdge(belong[i][j],belong[i][j+1],0,INF); } } for(int j=1;j<=Q;j++) { for(int i=1;i<=P-1;i++) { int x; scanf("%d",&x); AddEdge(belong[i][j],belong[i+1][j],-x,1); AddEdge(belong[i][j],belong[i+1][j],0,INF); } } for(int i=1;i<=a;i++) { int num,x,y; scanf("%d%d%d",&num,&x,&y); AddEdge(S,belong[x+1][y+1],0,num); } for(int i=1;i<=b;i++) { int num,x,y; scanf("%d%d%d",&num,&x,&y); AddEdge(belong[x+1][y+1],T,0,num); } MCMF(); return 0; }
