cnblogs
belong
“cnblogs” 和 ”blong“的最长公共子序列为4
方法1-->枚举
将长度为M和N的长度的字符串进行匹配,需要匹配2M * 2N次,复杂度为指数级
方法2-->动态规划
Step1->计算公共子序列长度
Step2->根据长度回溯求出最长公共子序列
现有两个序列X={x1,x2,x3,,,xi},Y={y1,y2,y3,,,yi}
设C[i,j]用于保存Xi与Yj的最长公共子序列长度
递推方程为->
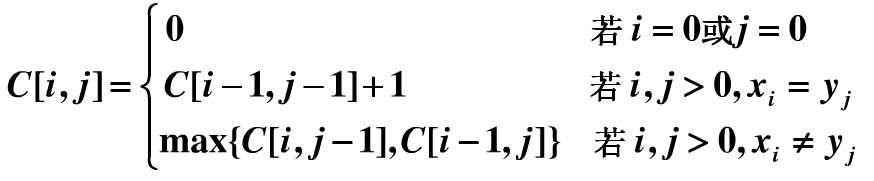
例如->

动态规划一个重要的性质便是解决‘子序列重叠问题’,避免重复计算
C[i,j]一直保存着当前(Xi,Yj)的最大子序列长度
C#代码-->
private static int calculateLCS(String s1, String s2) { int len_s1 = s1.Length; int len_s2 = s2.Length; int[,] C = new int[len_s2 + 1, len_s1 + 1]; for (int i=0;i<=len_s2;i++) { C[i, 0] = 0; } for (int j=0;j<=len_s1;j++) { C[0, j] = 0; } for (int i=1;i<=len_s2;i++) { for(int j= 1;j<=len_s1;j++) { if (s2[i-1] == s1[j-1]) { C[i, j] = C[i - 1, j - 1] + 1; } else { C[i, j] = Math.Max(C[i - 1, j], C[i, j - 1]); } Console.Write(C[i, j]+" "); } Console.WriteLine(""); } return C[len_s2,len_s1]; }
结果-->

