优先队列(priority queue)
是一种用来维护一组数据集合S的数据结构。
每一个元素都有一个相关的值,被称为关键字key。
这里以实现最大优先队列为例子
最大优先队列支持的操作如下:
INSERT(S,x):把元素x插入集合S中
MAXIMUN(S):返回S中具有最大键字的元素。
EXTRACT-MAX(S):去掉并且返回S中具有最大键字的元素。
INCREASE-KEY(S,x,k):将元素x的关键字增加到k(k>=x)
下面对于最大优先队列的具体实现进行描述。
首先,最大优先队列是基于堆的,所以其相关的建立堆、维护堆操作在这里不赘述。详见上一篇随笔。
heap_maximun(arr,heap_size):在O(1)的时间内实现MAXIMUN(S)的操作。
1 int heapmax(int arr[]) 2 { 3 return arr[1];//返回堆顶 4 }
heap_extract_max(arr,heap_size):实现EXTRACT-MAX(S)的操作。吐出堆顶元素,并且把堆顶位置元素与最后一个位置的元素交换,heap_size减1,而后调用维护堆(max_heapify)函数对堆进行调整。使其在吐出一个元素之后仍然满足大根堆的性质。
1 int heap_extract_max(int arr[],int &heap_size)//去掉并返回arr中具有最大键字的元素 2 { 3 if(heap_size<1) // 4 { 5 cout<<"heap underflow"<<endl; 6 return -1; 7 } 8 int max_=arr[1]; 9 arr[1]=arr[heap_size]; 10 heap_size--; 11 max_heapify(arr,1,heap_size); 12 return max_; 13 }
heap_increase_key(arr,x,k,heap_size):实现INCREASE-KEY(S,x,k)的操作。把元素x的关键字值增加到key,假设k的值不小于x原本关键字的值。在优先队列中,其元素由下标x来标识;而增大arr[i]的关键字有可能会违反最大堆的性质。所以在这个算法中,使用了【插入循环】的方式,从当前结点到根结点的路径上寻找新增关键字恰当的插入位置。
该过程会使结点x与其父结点的值比较。如果当前元素的关键字比较大,则交换当前元素与父结点元素的值。直到当前元素的关键字的值小于父元素关键字的值为止,此时已重新符合大根堆的性质。
如下图,显示了heap_increase_key的操作过程。(图截自算法导论)
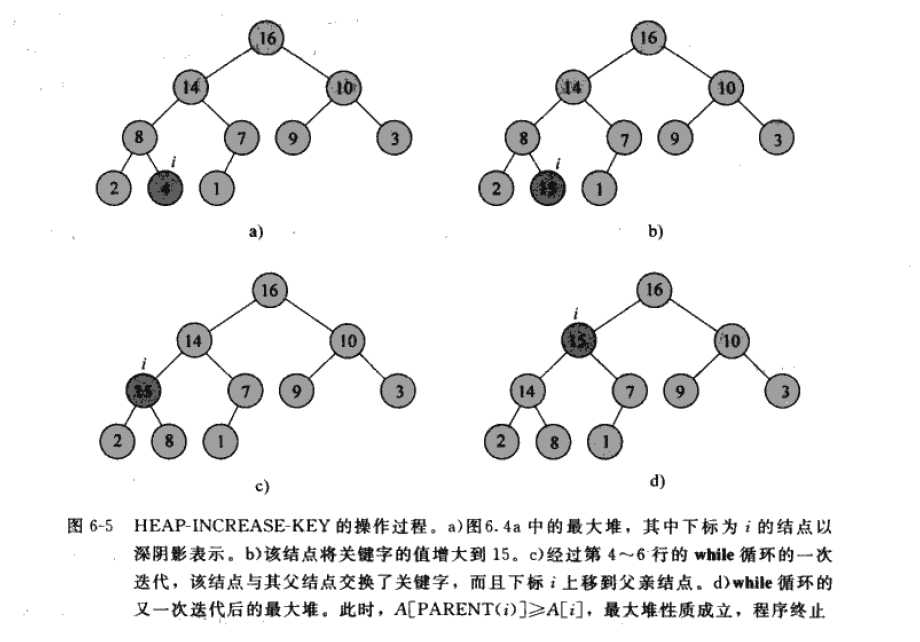
int heap_increase_key(int arr[],int x,int k,int heap_size)//把元素x的关键字值增加到key,假设k的值不小于x原本关键字的值 { if(k<arr[x]) { cout<<"new key is smaller than current key"; } arr[x]=k; while(x>1&&arr[x/2]<arr[x])//插入值x的粑粑比崽值小,于是交换元素值 { swap(arr[x/2],arr[x]); x=x/2; } }
max_heap_insert:在原来队列的基础上新增一个元素。这个算法通过先增加一个值为负无穷的关键字作为叶结点来扩展最大堆,而后调用heap_increase_key来为新的结点设置对应的关键字,保持大根堆的性质。
1 void max_heap_insert(int arr[],int k,int &heap_size)//把元素x值插入到集合中 2 { 3 heap_size++; 4 arr[heap_size]=-1;//通过增加一个关键字为负无穷的叶节点来扩展最大堆,这里用-1代替 5 heap_increase_key(arr,heap_size,k,heap_size); 6 }
总实现代码如下:
1 #include<iostream> 2 #include<algorithm> 3 #include<cstdlib> 4 using namespace std; 5 void max_heapify(int arr[],int i,int heap_size)//维护堆 6 { 7 int largest; 8 int left=2*i; 9 int right=2*i+1; 10 if(left<=heap_size&&arr[left]>arr[i]) largest=left; 11 else largest=i; 12 if(right<=heap_size&&arr[right]>arr[largest]) 13 largest=right; 14 if(largest!=i) 15 { 16 swap(arr[largest],arr[i]); 17 max_heapify(arr,largest,heap_size); 18 } 19 } 20 void build_max_heap(int arr[],int length)//建立堆 21 { 22 int heap_size=length; 23 for(int i=length/2; i>=1; i--) 24 { 25 max_heapify(arr,i,heap_size); 26 } 27 } 28 void heapsort(int arr[],int length) 29 { 30 int heap_size=length; 31 build_max_heap(arr,length); 32 for(int i=length; i>=2; i--) 33 { 34 swap(arr[1],arr[i]); 35 heap_size--; 36 max_heapify(arr,1,heap_size); 37 } 38 } 39 int heapmax(int arr[]) 40 { 41 return arr[1];//返回堆顶 42 } 43 int heap_extract_max(int arr[],int &heap_size)//去掉并返回arr中具有最大键字的元素 44 { 45 if(heap_size<1) // 46 { 47 cout<<"heap underflow"<<endl; 48 return -1; 49 } 50 int max_=arr[1]; 51 arr[1]=arr[heap_size]; 52 heap_size--; 53 max_heapify(arr,1,heap_size); 54 return max_; 55 } 56 int heap_increase_key(int arr[],int x,int k,int heap_size)//把元素x的关键字值增加到key,假设k的值不小于x原本关键字的值 57 { 58 if(k<arr[x]) 59 { 60 cout<<"new key is smaller than current key"; 61 } 62 arr[x]=k; 63 while(x>1&&arr[x/2]<arr[x])//插入值x的粑粑比崽值小,于是交换元素值 64 { 65 swap(arr[x/2],arr[x]); 66 x=x/2; 67 } 68 } 69 void max_heap_insert(int arr[],int k,int &heap_size)//把元素x值插入到集合中 70 { 71 heap_size++; 72 arr[heap_size]=-1;//通过增加一个关键字为负无穷的叶节点来扩展最大堆,这里用-1代替 73 heap_increase_key(arr,heap_size,k,heap_size); 74 } 75 void show(int arr[],int heap_size) 76 { 77 cout<<"show the heap:"; 78 for(int i=1; i<=heap_size; i++) 79 { 80 cout<<arr[i]<<" "; 81 } 82 cout<<endl; 83 } 84 int main() 85 { 86 int arr[]= {0,5,6,8,99,102,3,54,76,89,21}; 87 int heap_size=10; 88 build_max_heap(arr,heap_size);//建堆 89 int maxn=heapmax(arr); 90 cout<<"the max data is:"<<maxn<<endl; 91 maxn=heap_extract_max(arr,heap_size); 92 cout<<"now the max data "<<maxn<<" was deleted."<<endl; 93 show(arr,heap_size); 94 heapsort(arr,heap_size); 95 cout<<"after sort and"; 96 show(arr,heap_size); 97 int i=6,key=80; 98 heap_increase_key(arr,i,key,heap_size);//把堆中第i个元素的值改为key值。 99 max_heap_insert(arr,100,heap_size);//插入新值100 100 show(arr,heap_size); 101 heapsort(arr,heap_size); 102 cout<<"after sort and"; 103 show(arr,heap_size); 104 return 0; 105 }
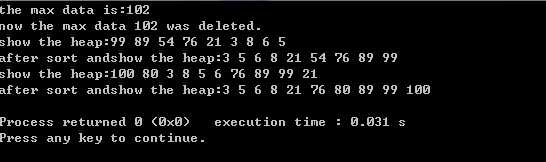
测试截图: