题目描述
星云中有n颗行星,每颗行星的位置是(x,y,z)。每次可以消除一个面(即x,y或z坐标相等)的行星,但是由于时间有限,求消除这些行星的最少次数。
输入输出格式
输入格式:
第1行为小行星个数n,第2行至第n+1行为xi, yi, zi,描述第i个小行星所在的位置。
输出格式:
共1行,为消除所有行星的最少次数。
输入输出样例
说明
1≤n≤50000
1≤x,y,z≤500
解:
看到数据范围,以及“消除”、“最少次数”的字样,就知道与最小割有关。问题在于怎么割呢?
要消除一颗小行星,可以从三个面来消除。xx 面,yy 面和 zz 面。不难想到,将这三个面上的每一个坐标建两个点——入点和出点。由入点向出点连一条容量为 11 的边。当入点和出点之间的这条边被割掉时,就说明是在这个面的这一个点消除了一次。
我们想要消除所有的小行星,就说明每一颗小行星在 xx 面,yy 面或 zz 面这三个面中,至少有一个面把它消除了。也就是说,不存在一条连通 x-y-zx?y?z 的路径,这就是割了。
于是我们对于每一颗小行星,从 xx 面的出点向 yy 面的入点连一条容量为 INFINF 的边(仅为保证点之间的连通性),从 yy 面的出点向 zz 面的入点连容量为 INFINF 的边。再从超级源向每个 xx 面的入点连容量为 INFINF 的边,从每个 zz 面的出点向超级汇连容量为 INFINF 的边。
建出来的图大致如下(样例):
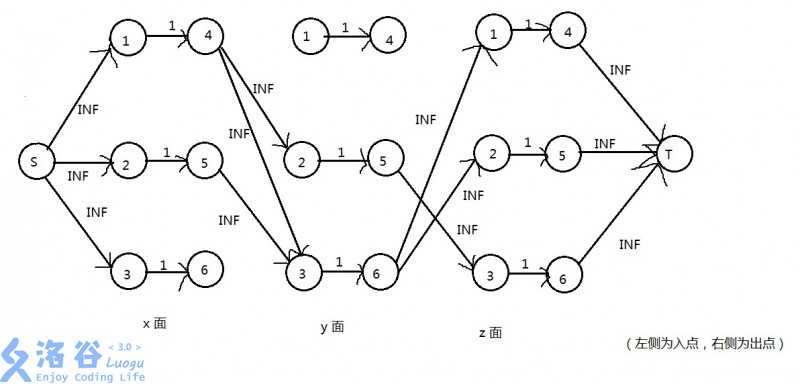
根据上面的分析,显然地,就是求 s-ts?t 最小割,这样就能保证每颗小行星都被消在某个面上。
但是……图好乱……
不难发现,这张图是可以简化的。注意到从超级源 SS 向每一个 xx 连出的边,下一条边都是从 xx 的入点向 xx 的出点连的一条容量为 11 的边。根据 Total Flow 一题可知,这两条边就类似于串联的关系,是可以合并的。
于是我们简化了这张图,改为直接从超级源 SS 向每个 xx (入点就可以不要了,于是就没有出入点之分了)连一条权值为 11 的边。从 zz 面的边到终点同理,也可以简化。
简化后的图大致如下:
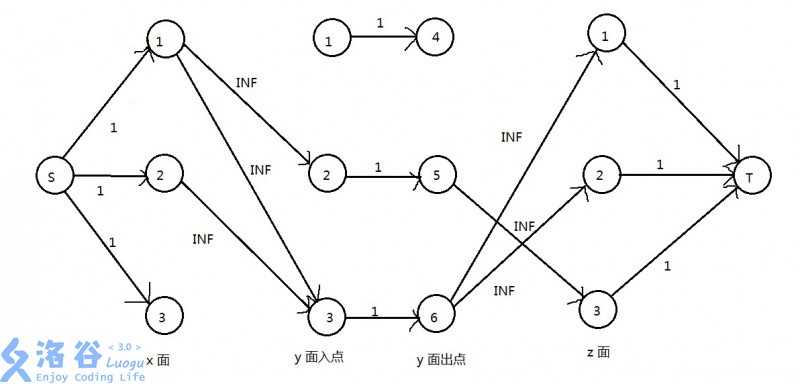
这样只要拆 yy 面的点就好了。是不是清爽多了?
最后求解该图的最小割即可。

1 #include<iostream> 2 #include<cstdio> 3 #include<algorithm> 4 #include<cmath> 5 #include<cstring> 6 #include<string> 7 #include<queue> 8 #include<map> 9 #define ll long long 10 #define DB double 11 #define inf 2147480000 12 using namespace std; 13 const int N=1e6+90; 14 struct node{ 15 int u,v,fl,ne; 16 }e[N]; 17 int h[N],tot; 18 void add1(int u,int v,int fl) 19 { 20 tot++;e[tot]=(node){u,v,fl,h[u]};h[u]=tot; 21 } 22 void add(int u,int v,int fl) 23 { 24 add1(u,v,fl);add1(v,u,0); 25 } 26 int q[N],d[N],hh,tt,S,T; 27 bool bfs() 28 { 29 for(int i=S;i<=T;++i) d[i]=0; 30 d[S]=1;hh=1;tt=0;q[++tt]=S; 31 while(hh<=tt) 32 { 33 int ff=q[hh];hh++; 34 for(int i=h[ff];i;i=e[i].ne) 35 { 36 int rr=e[i].v; 37 if(!d[rr] && e[i].fl) 38 d[rr]=d[ff]+1,q[++tt]=rr; 39 } 40 } 41 return d[T]; 42 } 43 int dfs(int u,int fl) 44 { 45 if(u==T || !fl) return fl; 46 int get=0,f; 47 for(int i=h[u];i;i=e[i].ne) 48 { 49 int rr=e[i].v; 50 if(d[rr]==d[u]+1 && e[i].fl) 51 { 52 f=dfs(rr,min(fl,e[i].fl)); 53 if(f==0) continue; 54 e[i].fl-=f;e[i^1].fl+=f; 55 get+=f;fl-=f; 56 if(fl==0) break; 57 } 58 } 59 if(get==0) d[u]=0; 60 return get; 61 } 62 int Flow() 63 { 64 int ans=0; 65 while(bfs()) ans+=dfs(S,inf); 66 return ans; 67 } 68 int n; 69 int main() 70 { 71 scanf("%d",&n); 72 S=0;T=500*4+1;tot=1; 73 for(int i=1;i<=500;++i) 74 { 75 add(S,i,1); 76 add(i+500*3,T,1); 77 } 78 for(int o=1,x,y,z;o<=n;++o) 79 { 80 scanf("%d%d%d",&x,&y,&z); 81 add(x,y+500,inf); 82 add(y+500,y+500*2,1); 83 add(y+500*2,z+500*3,inf); 84 } 85 cout<<Flow(); 86 return 0; 87 }

