JZOJ3966 Sabotage 题解

Description
FJ 的死对头，FP，现在决定了去破坏FJ 的挤奶设备！
这个挤奶设备由一行N（3 <= N<= 100, 000）个挤奶机器，其中第i 个机器生产Mi 单位的牛奶（1<= Mi <= 10, 000）。FP 计划将机器连续的一块断开——从第i 个机器到第j 个机器（2<= i<= j<= N-1）；注意第一个和最后一个机器FJ 并不想要断开，因为这会让这次事件太容易被发现。FP 的目标是让剩下的机器的牛奶平均产量最小。FP 打算移去至少一台机器，即使对他来说不进行破坏更好。
幸运的是，FJ 已获悉FP 的邪恶计划，并且他想知道如果计划成功他的挤奶设备会被破坏成什么样。请帮助FJ 找到，如果FP 成功，最小的剩下挤奶机器的平均生产量。

Input
第一行：整数N。
第2 至N + 1 行：第i + 1 行包含Mi。

Output
输出单独一行一个整数——FP 能获得的最小的可能的平均数，四舍五入到小数点后3 位数字，小数点后三位数字都要输出。

Sample Input
5
5
1
7
8
2

Sample Output
2.667
样例解释：
最佳方案是移除7 和8，留下5; 1 以及2，使得平均值为8/3。

Data Constraint
对于14% 的数据，有N<=10。
对于49% 的数据，有N <=1000。

思路：二分答案。当然这题还有别的做法，二分只是其中一种。我们直接二分答案，问题就是如何check。
设数列里前i位的和（也就是前缀和）是sum[i]，那么显然[l,r]的和就是sum[r] - sum[l - 1]。对于一个二分出来的答案k，如果去掉区间[l,r]后的平均数比k更小，那么k就可行。
也就是：

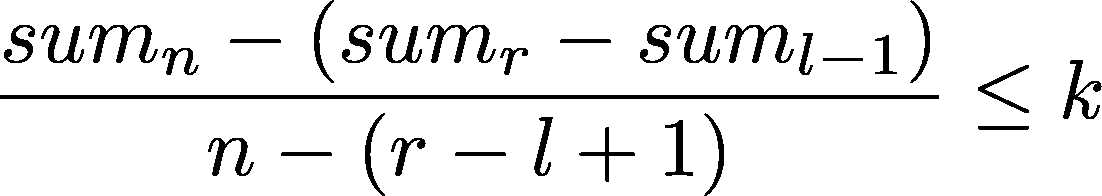
稍微进行一下移项能得到：

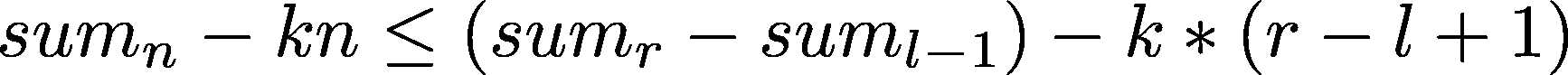
观察不等式左右，sumn减去了n个k，也就相当于原来的每个数都减去k再求一次前缀和。[l,r]的区间和减去了(r - l + 1)个k，也是每个数减掉了k，所以我们把原数列的数全部减去k，然后去掉有关k的项得：

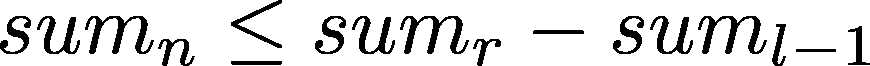
右边是一段区间的和，为了使不等式尽可能成立，我们需要另不等式右边最大，也就演变成了最大子段和问题了。
于是就非常好写了。
代码：

#include <cmath>
#include <cstdio>
#include <cstring>
#include <cstdlib>

const int N = 1e5 + 3;
const double EXP = 1e-12; //烦人的精度

int n;
double l, r, mid, ans = -1.0, a[N];

int check(double x)
{
    double ret = 0, sum = 0.0, maxx = -1e9;
    for (int i = 1; i <= n; i++) ret += a[i] - x; //先把每个数都减去二分的答案
    for (int i = 2; i <= n - 1; i++)
    {
        if (sum < 0) sum = 0;
        sum += a[i] - x;
        if (sum > maxx) maxx = sum;
    }
    return ret <= maxx;
}

int main()
{
    scanf("%d", &n);
    for (int i = 1; i <= n; i++) scanf("%lf", a + i);
    l = 1.0, r = n * 10000.0;
    while (r - l >= EXP)
    {
        mid = (l + r) / 2;
        if (check(mid)) r = mid, ans = mid;
        else l = mid;
    }
    printf("%.3lf\n", ans);
    return 0;
}