久仰K-D tree大名已久,终于在合适的时候遇见了合适的水题入了坑入了门
K-D tree是什么
K-D tree是什么? 按名字上翻译来就是K维的树,就是一个用来维护K维空间的点的平衡二叉树
K-D tree有什么用
K-D tree可以进行空间上的操作,最经典的就是查询最近/最远 点对
还有很多我不知道
K-D tree的原理与实现
K-D tree,又有一个名字叫做划分树,与其原理相联系
类似于普通的平衡树,对于普通的平衡树的节点u,其左右子树分别是权值小于u的和权值大于u的,该节点就相当于在一个值域上在u的值处进行了分割
而kd-tree对于多维空间进行分割,一个节点储存着以下信息:
struct node{
int d[K],s[2],x[2],y[2],......;
}e[maxn];d就是该节点储存的点的K维坐标
s储存着其左右儿子
剩余的若干数组储存着以该节点为根的子树的各维度的最值
也就是说,一棵子树实际上对应着一个空间区域,而根节点将该空间区域划分为左右两部分
而该空间的信息就储存在子树的根节点中
但是这是在一个多维空间,将空间区域划分有多种方式
一般地,kd-tree垂直于其中一个坐标轴将平面划分开
以2维为例,如下图所示
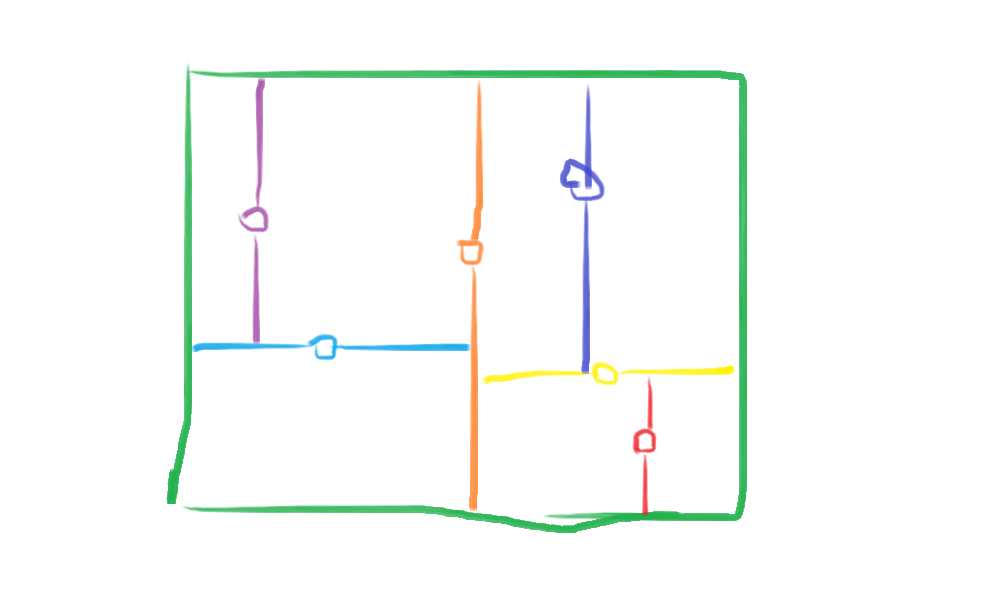
如图圆圈表示节点,将区域进行划分
一般遵循以下规律构造:
①各层节点交替划分各维空间
根节点划分x坐标
其儿子划分y坐标
其孙子划分z坐标
......
②每一层的区域中,按该层划分的坐标排序,选取其中位数作为划分点进行划分
切点作为父节点,左边的点划分到左子树中,右边的点划分到右子树中
③逐层划分,直至划分区域无节点
在C++的STL中,有一个函数nth_element()可以在\(O(n)\)时间内将一个数组第k大找出,并将小于的放在左边,大于的放在右边
具体实现类似快排
对于K维空间,建树复杂度\(O(Knlogn)\)
二维建树代码如下:
#define ls e[u].s[0]
#define rs e[u].s[1]
#define cmin(x,y) (x > y ? x = y : x)
#define cmax(x,y) (x < y ? x = y : x)
struct point{int d[2];}a[maxn];
struct node{int d[2],s[2],x[2],y[2];}e[maxn];
int n,rt,D,x,y;
bool operator <(const point& a,const point& b){
return a.d[D] == b.d[D] ? a.d[D ^ 1] < b.d[D ^ 1] : a.d[D] < b.d[D];
}
void pup(int u){
if (ls){
cmin(e[u].x[0],e[ls].x[0]); cmax(e[u].x[1],e[ls].x[1]);
cmin(e[u].y[0],e[ls].y[0]); cmax(e[u].y[1],e[ls].y[1]);
}
if (rs){
cmin(e[u].x[0],e[rs].x[0]); cmax(e[u].x[1],e[rs].x[1]);
cmin(e[u].y[0],e[rs].y[0]); cmax(e[u].y[1],e[rs].y[1]);
}
}
int build(int l,int r,int d){
D = d; int u = l + r >> 1;
nth_element(a + l,a + u,a + r + 1);
e[u].d[0] = e[u].x[0] = e[u].x[1] = a[u].d[0];
e[u].d[1] = e[u].y[0] = e[u].y[1] = a[u].d[1];
if (l < u) ls = build(l,u - 1,d ^ 1);
if (r > u) rs = build(u + 1,r,d ^ 1);
pup(u);
return u;
}查询最近/远点对
以最近为例
与普通的暴力不同,在KDtree中查询最近点对,预期复杂度为\(O(logn)\),可以被卡为\(O(\sqrt{N})\)
我们到一个节点时,用该节点更新答案,并计算左右子树的估价函数
由于每棵子树都对应一个区域,可以由此计算出每棵子树的最近值
如果最近的点的贡献都比当前答案大,那么就不用访问该子树了
以2维为例,估价函数可以这样写:
#define getd(u) (max(x - e[u].x[1],0) + max(e[u].x[0] - x,0) + max(y - e[u].y[1],0) + max(e[u].y[0] - y,0))
#define getdx(u) (max(abs(e[u].x[0] - x),abs(e[u].x[1] - x)) + max(abs(e[u].y[0] - y),abs(e[u].y[1] - y)))实际上就是求与四个顶点距离的最值
由此可以写出搜索函数:
void qmx(int u){
LL t = equal(u) ? -INF : (abs(e[u].d[0] - x) + abs(e[u].d[1] - y)),d[2];
if (ls) d[0] = getdx(ls); else d[0] = -INF;
if (rs) d[1] = getdx(rs); else d[1] = -INF;
cmax(mx,t); t = d[0] <= d[1];
if (d[t] > mx) qmx(e[u].s[t]); t ^= 1;
if (d[t] > mx) qmx(e[u].s[t]);
}
void qmn(int u){
int t = equal(u) ? INF : (abs(e[u].d[0] - x) + abs(e[u].d[1] - y)),d[2];
if (ls) d[0] = getd(ls); else d[0] = INF;
if (rs) d[1] = getd(rs); else d[1] = INF;
cmin(mn,t); t = d[0] >= d[1];
if (d[t] < mn) qmn(e[u].s[t]); t ^= 1;
if (d[t] < mn) qmn(e[u].s[t]);
}例题
由以上基础,我们就可以轻松A掉SDOI2010 hideseek了
用每个点搜一次就好
#include<iostream>
#include<cstdio>
#include<cmath>
#include<cstring>
#include<algorithm>
#define LL long long int
#define Redge(u) for (int k = h[u],to; k; k = ed[k].nxt)
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define BUG(s,n) for (int i = 1; i <= (n); i++) cout<<s[i]<<‘ ‘; puts("");
#define ls e[u].s[0]
#define rs e[u].s[1]
#define cmin(x,y) (x > y ? x = y : x)
#define cmax(x,y) (x < y ? x = y : x)
#define getd(u) (max(x - e[u].x[1],0) + max(e[u].x[0] - x,0) + max(y - e[u].y[1],0) + max(e[u].y[0] - y,0))
#define getdx(u) (max(abs(e[u].x[0] - x),abs(e[u].x[1] - x)) + max(abs(e[u].y[0] - y),abs(e[u].y[1] - y)))
#define equal(u) (e[u].d[0] == x && e[u].d[1] == y)
using namespace std;
const int maxn = 100005,maxm = 100005,INF = 2100000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57){if (c == ‘-‘) flag = -1; c = getchar();}
while (c >= 48 && c <= 57){out = (out << 3) + (out << 1) + c - 48; c = getchar();}
return out * flag;
}
struct point{int d[2];}a[maxn];
struct node{int d[2],s[2],x[2],y[2];}e[maxn];
int n,rt,D,x,y; LL mx,mn;
bool operator <(const point& a,const point& b){
return a.d[D] == b.d[D] ? a.d[D ^ 1] < b.d[D ^ 1] : a.d[D] < b.d[D];
}
void pup(int u){
if (ls){
cmin(e[u].x[0],e[ls].x[0]); cmax(e[u].x[1],e[ls].x[1]);
cmin(e[u].y[0],e[ls].y[0]); cmax(e[u].y[1],e[ls].y[1]);
}
if (rs){
cmin(e[u].x[0],e[rs].x[0]); cmax(e[u].x[1],e[rs].x[1]);
cmin(e[u].y[0],e[rs].y[0]); cmax(e[u].y[1],e[rs].y[1]);
}
}
int build(int l,int r,int d){
D = d; int u = l + r >> 1;
nth_element(a + l,a + u,a + r + 1);
e[u].d[0] = e[u].x[0] = e[u].x[1] = a[u].d[0];
e[u].d[1] = e[u].y[0] = e[u].y[1] = a[u].d[1];
if (l < u) ls = build(l,u - 1,d ^ 1);
if (r > u) rs = build(u + 1,r,d ^ 1);
pup(u);
return u;
}
void qmx(int u){
LL t = equal(u) ? -INF : (abs(e[u].d[0] - x) + abs(e[u].d[1] - y)),d[2];
if (ls) d[0] = getdx(ls); else d[0] = -INF;
if (rs) d[1] = getdx(rs); else d[1] = -INF;
cmax(mx,t); t = d[0] <= d[1];
if (d[t] > mx) qmx(e[u].s[t]); t ^= 1;
if (d[t] > mx) qmx(e[u].s[t]);
}
void qmn(int u){
int t = equal(u) ? INF : (abs(e[u].d[0] - x) + abs(e[u].d[1] - y)),d[2];
if (ls) d[0] = getd(ls); else d[0] = INF;
if (rs) d[1] = getd(rs); else d[1] = INF;
cmin(mn,t); t = d[0] >= d[1];
if (d[t] < mn) qmn(e[u].s[t]); t ^= 1;
if (d[t] < mn) qmn(e[u].s[t]);
}
int main(){
n = read();
for (int i = 1; i <= n; i++) a[i].d[0] = read(),a[i].d[1] = read();
rt = build(1,n,0);
LL ans = INF;
for (int i = 1; i <= n; i++){
x = a[i].d[0]; y = a[i].d[1];
mx = 0; qmx(rt);
mn = INF; qmn(rt);
ans = min(ans,mx - mn);
}
printf("%lld\n",ans);
return 0;
}