全向轮底盘上安装两条磁传感器带用于磁导轨寻迹
如简图所示,两条与Y直线相交的黑色线条我们认为是两条磁检测传感器带
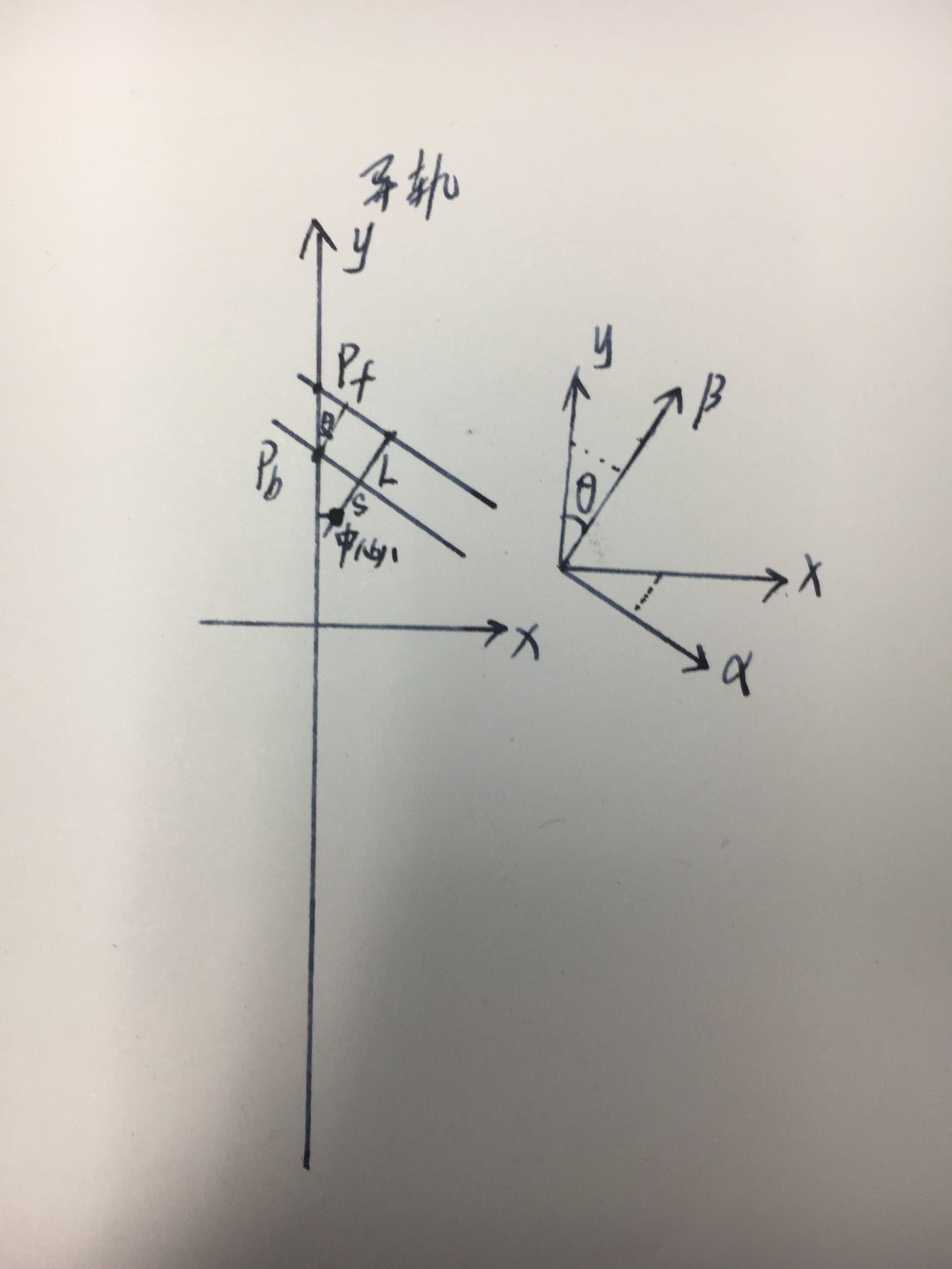
矢量方法修正车体位置
定义轨道左为负向,轨道右为正向。传感器左检测为负,右检测为正;
定义底盘坐标系为αβ,轨道坐标系为XY,车体与轨道坐标系的偏转角度为θ;
设前传感器检测为值为Pf,后传感器检测位置为Pb,两传感器距离为L,后传感器与机器人中心点的距离为S(如中心在两传感器中间,S符号为负,如中心在后传感器后面,S符号为正)。中心点旋转偏角为θ,横向偏移为Poff。
由几何关系可得出θ = tan-1((Pb-Pf)/L)
Poff = (-Pb/tanθ-S)sinθ
然后通过转换关系(诸如PID,模糊等方式)将θ 转换为对应的底盘自旋速度Vθ (注意正反转符号),Poff 转换为对应的磁导轨X轴速度矢量Voff (注意Voff 带有方向),再分解为建立到车体上的αβ速度坐标系Voff sinθ 、Voff cosθ 。
此外底盘还有沿磁导轨Y轴方向的运动速度V,该速度同样由建立到车体上的αβ速度坐标系合成,V sinθ 、V cosθ
则传递到电机速度解算函数的速度参数
Vβ = -Voff sinθ + V cosθ
Vα = -Voff cosθ - V sinθ
Vω = Vθ
上面的分析只考虑了底盘实际位置的横移与旋转,没有考虑当前畸变的速度方向的影响,对于车体沿导轨的主速度采用了直接修正的方式去处理,这里忽略了一个情况,速度不是瞬变的,车体受惯性仍会沿当前主速度方向运动,这样即使修正了主速度矢量与导轨Y方向对齐,但原来偏离了θ‘角度的主速度仍会影响车体运动。一般来说θ‘会在0到θ之间,要具体求出需要获取当前各个轮子的速度,然后通过坐标换算反求。为了抵消这个原主速度的影响并简化计算,我们可以在Voff上再叠加一个修正速度,这个速度受上一个主速度大小和θ影响。
这样新的Voffsum =Voff +kVlastsinθ
k为修正系数
这样修正上面的传递到电机速度解算函数的速度参数
Vβ = -Voffsum sinθ + V cosθ
Vα = -Voffsum cosθ - V sinθ
Vω = Vθ
