首先我们先来看一个由普通数组构建的普通堆。
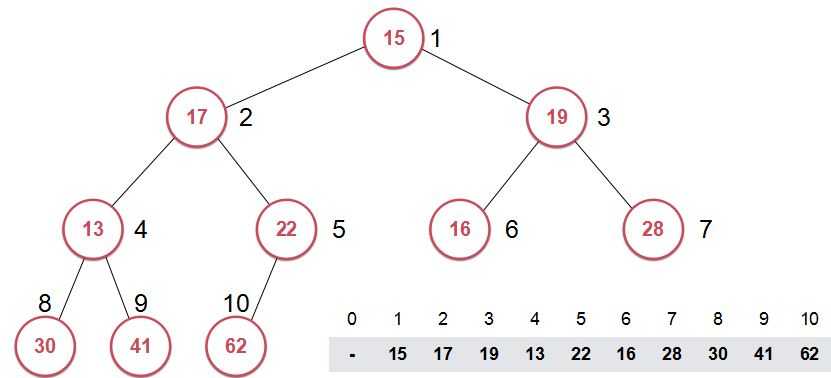
然后我们通过前面的方法对它进行堆化(heapify),将其构建为最大堆。
结果是这样的:
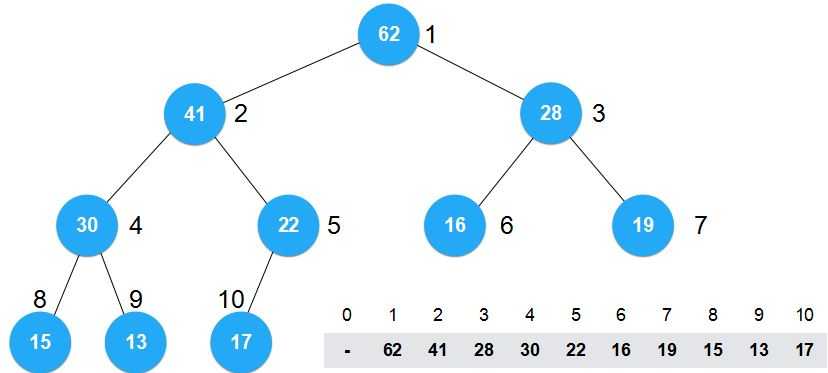
对于我们所关心的这个数组而言,数组中的元素位置发生了改变。正是因为这些元素的位置发生了改变,我们才能将其构建为最大堆。
可是由于数组中元素位置的改变,我们将面临着几个局限性。
1.如果我们的元素是十分复杂的话,比如像每个位置上存的是一篇10万字的文章。那么交换它们之间的位置将产生大量的时间消耗。(不过这可以通过技术手段解决)
2.由于我们的数组元素的位置在构建成堆之后发生了改变,那么我们之后就很难索引到它,很难去改变它。例如我们在构建成堆后,想去改变一个原来元素的优先级(值),将会变得非常困难。
可能我们在每一个元素上再加上一个属性来表示原来位置可以解决,但是这样的话,我们必须将这个数组遍历一下才能解决。(性能低效)
针对以上问题,我们就需要引入索引堆(Index Heap)的概念。
对于索引堆来说,我们将数据和索引这两部分分开存储。真正表征堆的这个数组是由索引这个数组构建成的。(像下图中那样,每个结点的位置写的是索引号)
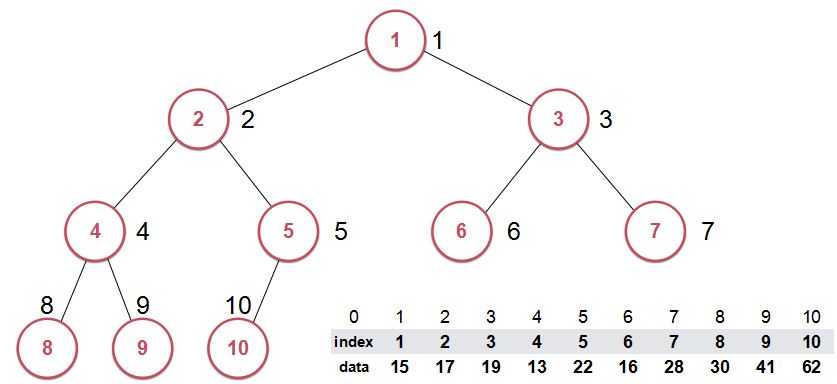
而在构建堆(以最大索引堆为例)的时候,比较的是data中的值(即原来数组中对应索引所存的值)
而构建完之后,data域并没有发生改变,位置改变的是index域。
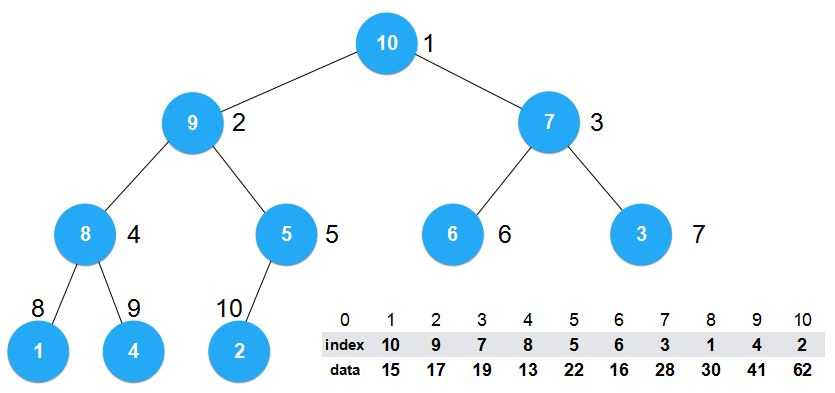
那么现在这个最大堆该怎么解读呢?
例如,堆顶元素为Index=10代表的就是索引为10的data域的值,即62。
这时我们来看,构建堆的过程就是简单地索引之间的交换,索引就是简单的int型。效率很高。
现在如果我们想对这个数组进行一些改变,比如我们想将索引为7的元素值改为100,那我们需要做的就是将索引7所对应data域的28改为100。时间复杂度为O(1)。
当然改完之后,我们还需要进行一些操作来维持最大堆的性质。不过调整的过程改变的依旧是index域的内容。
