题目
你的公司接到了一批订单。订单要求你的公司提供n类产品,产品被编号为1~n,其中第i类产品共需要Ci件。公司共有m名员工,员工被编号为1~m员工能够制造的产品种类有所区别。一件产品必须完整地由一名员工制造,不可以由某名员工制造一部分配件后,再转交给另外一名员工继续进行制造。
我们用一个由0和1组成的m*n的矩阵A来描述每名员工能够制造哪些产品。矩阵的行和列分别被编号为1~m和1~n,Ai,j为1表示员工i能够制造产品j,为0表示员工i不能制造产品j。
如果公司分配了过多工作给一名员工,这名员工会变得不高兴。我们用愤怒值来描述某名员工的心情状态。愤怒值越高,表示这名员工心情越不爽,愤怒值越低,表示这名员工心情越愉快。员工的愤怒值与他被安排制造的产品数量存在某函数关系,鉴于员工们的承受能力不同,不同员工之间的函数关系也是有所区别的。
对于员工i,他的愤怒值与产品数量之间的函数是一个Si+1段的分段函数。当他制造第1~Ti,1件产品时,每件产品会使他的愤怒值增加Wi,1,当他制造第Ti,1+1~Ti,2件产品时,每件产品会使他的愤怒值增加Wi,2……为描述方便,设Ti,0=0,Ti,si+1=+∞,那么当他制造第Ti,j-1+1~Ti,j件产品时,每件产品会使他的愤怒值增加Wi,j, 1≤j≤Si+1。
你的任务是制定出一个产品的分配方案,使得订单条件被满足,并且所有员工的愤怒值之和最小。由于我们并不想使用Special Judge,也为了使选手有更多的时间研究其他两道题目,你只需要输出最小的愤怒值之和就可以了。
输入格式
第一行包含两个正整数m和n,分别表示员工数量和产品的种类数;
第二行包含n 个正整数,第i个正整数为Ci;
以下m行每行n 个整数描述矩阵A;
下面m个部分,第i部分描述员工i的愤怒值与产品数量的函数关系。每一部分由三行组成:第一行为一个非负整数Si,第二行包含Si个正整数,其中第j个正整数为Ti,j,如果Si=0那么输入将不会留空行(即这一部分只由两行组成)。第三行包含Si+1个正整数,其中第j个正整数为Wi,j。
输出格式
仅输出一个整数,表示最小的愤怒值之和。
输入样例
2 3
2 2 2
1 1 0
0 0 1
1
2
1 10
1
2
1 6
输出样例
24
提示
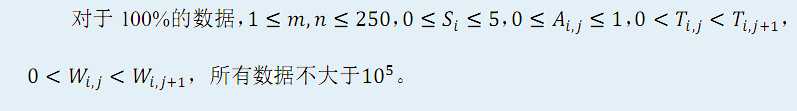
题解
挺裸的建图
#include<iostream>
#include<cstdio>
#include<cstring>
#include<queue>
#include<algorithm>
#define LL long long int
#define REP(i,n) for (int i = 1; i <= (n); i++)
#define Redge(u) for (int k = h[u]; k != -1; k = ed[k].nxt)
using namespace std;
const int maxn = 505,maxm = 5000005,INF = 1000000000;
inline int read(){
int out = 0,flag = 1; char c = getchar();
while (c < 48 || c > 57) {if (c == ‘-‘) flag = -1; c = getchar();}
while (c >= 48 && c <= 57) {out = (out << 1) + (out << 3) + c - ‘0‘; c = getchar();}
return out * flag;
}
int h[maxn],ne,S,T,p[maxn];
LL minf[maxn],d[maxn];
bool inq[maxn];
struct EDGE{int from,to,nxt; LL f,w;}ed[maxm];
inline void build(int u,int v,LL f,LL w){
ed[ne] = (EDGE){u,v,h[u],f,w}; h[u] = ne++;
ed[ne] = (EDGE){v,u,h[v],0,-w}; h[v] = ne++;
}
LL mincost(){
queue<int> q; int u,to; LL flow = 0,cost = 0;
while (true){
for (int i = 0; i <= T; i++) d[i] = INF,inq[i] = false,minf[i] = INF;
d[S] = 0; q.push(S);
while (!q.empty()){
u = q.front(); q.pop();
inq[u] = false;
Redge(u) if (ed[k].f && d[to = ed[k].to] > d[u] + ed[k].w){
d[to] = d[u] + ed[k].w; p[to] = k; minf[to] = min(minf[u],ed[k].f);
if (!inq[to]) q.push(to),inq[to] = true;
}
}
if (d[T] == INF) break;
flow += minf[T]; cost += minf[T] * d[T];
u = T;
while (u){
ed[p[u]].f -= minf[T]; ed[p[u]^1].f += minf[T];
u = ed[p[u]].from;
}
}
return cost;
}
int n,m,L[10],W[10];
int main(){
memset(h,-1,sizeof(h));
m = read(); n = read(); S = 0; T = n + m + 1;
for (int i = 1; i <= n; i++) build(m + i,T,read(),0);
for (int i = 1; i <= m; i++)
for (int j = 1; j <= n; j++)
if (read()) build(i,m + j,INF,0);
for (int i = 1; i <= m; i++){
int t = read();
for (int j = 1; j <= t; j++) L[j] = read();
for (int j = 1; j <= t; j++) build(S,i,L[j] - L[j - 1],read());
build(S,i,INF,read());
}
printf("%lld\n",mincost());
return 0;
}