1、旋转矩阵
注:旋转矩阵标题下涉及到的SLAM均不包含位移。
根据同一点P在不同坐标系下e(e1,e2,e3)e‘(e1‘,e2‘,e3‘)的坐标a(a1,a2,a3)a‘(a1‘,a2‘,a3‘)有如下等式成立:
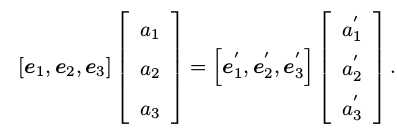

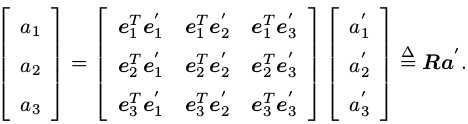
即a = eTe‘a‘,其中eTe‘设为R为旋转矩阵,即a = Ra‘,由此便得到P在e‘坐标系下到e坐标系下的坐标变换。
在SLAM中一般a‘为相机坐标系下坐标Pc,a为世界坐标系下坐标Pw。则有Pw = RPc
其中R = eTe‘ → eR = e‘
如果把R分成三个列向量,则每个列向量即为e’坐标系的基在e坐标系下的坐标。
与此对应SLAM中即为相机坐标系下的坐标轴在世界坐标系下的坐标。
(a11,a21,a31)即为基e1‘在e坐标系下的坐标(e‘坐标系的另两个基e2‘,e3‘亦如此)。
与此对应的slam中即为相机坐标系下x坐标轴在世界坐标系下的坐标。
SLAM中这里的R一般被称为相机的姿态(不是位姿,不包含平移)。
