集成学习中还有一个重要的类别是Boosting，这个是基学习器具有较强依赖串行而成的算法，目前主流的主要有三个算法：GBDT，Adaboost，XGBoost

这个链接可以看看：https://www.cnblogs.com/willnote/p/6801496.html

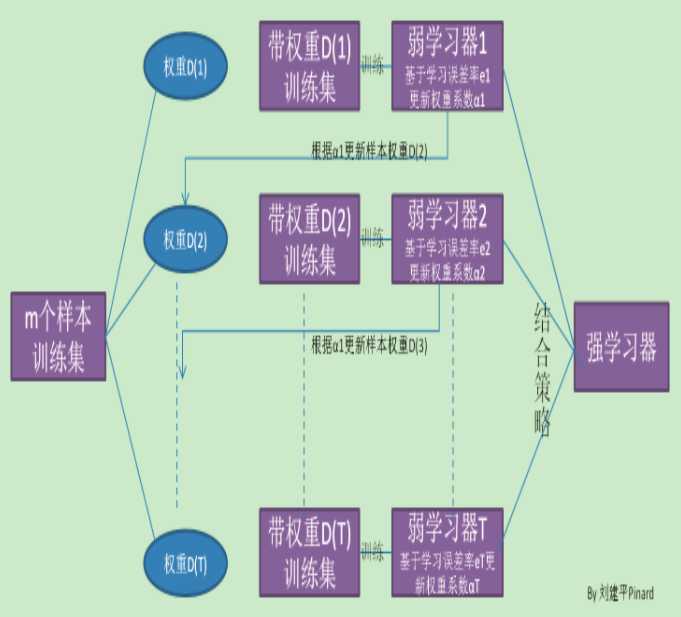
boosting算法的原理如下：

1、GBDT

2、XGBoost

3、Adaboost

 Adaboost的基本思想是这样的：

1、一开始所有的样本权重全部相等，训练处第一个基分类器，根据这个基分类器对样本进行划分

2、从第二轮开始针对前一轮的分类结果重新赋予样本权重，对于分类错误的样本权重加大，正确的样本权重减少。

3、之后根据新得到样本的权重指导本轮中的基分类器训练，即在考虑样本不同权重的情况下得到本轮错误率最低的基分类器。重复以上步骤直至训练到约定的轮数结束，每一轮训练得到一个基分类器。

可以想象到，远离边界（超平面）的样本点总是分类正确，而分类边界附近的样本点总是有大概率被弱分类器（基分类器）分错，所以权值会变高，即边界附近的样本点会在分类时得到更多的重视。

步骤说明：

1）分类问题

1、对于所有的样本，我们先赋予初始权重，分别都相等1/M

2、选择一个基分类器对样本进行分类，计算经过这个基分类器分类后的误差率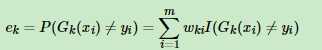，其中w为样本权重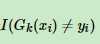，这个函数表示若预测值与实际值不一致返回1，否则返回0

经过以上的计算，就会计算出所有分类错的样本的误差率

3、计算这个基学习器的权重系数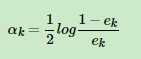：，这个公式说明：如果误差率e_k越小，那么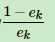越大，那么log之后也越大，因此这个系数a_k也越大，这说明如果误差率越小，学习期的系数权重越大（注意跟下面的样本系数不一样啊！！！）

4、更新样本的权重，把错分的权重加大，正确的权重减小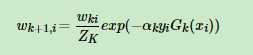其中Z_K是规范化因子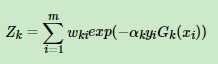

这里先解释第一个公式，也就是权重公式：e^x函数图像可以去百度一下，是一个过0,1点的递增函数，也就是如果分类错误，那么yi*Gk（xi）就不是同号就<0，那么这个就会比较大，大于1，也就是原来的权重基础上乘以一个比1大的数字，调大了这个权重，同理，如果分类正确就会调小，也就是，如果分错了，误差率变大了，样本权重变大（记住跟系数权重不一样啊！！！）

第二个公式是规范化因子，因为如果不除以这个因子，会导致权重总和不等于1，除掉这个因子之后所有权重加起来又等于1了

5、根据不同权重的样本在做第二个基分类器，同样计算权重，一直轮

6、最后通过训练出来的K个分类器进行决策：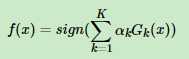

2）回归问题

回归问题不同的是误差率的计算：

1、对于所有的样本，我们先赋予初始权重，分别都相等1/M

2、选择一个基学习期进行学习，得到第一个模型

首先计算最大误差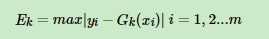：，接着计算每个样本的相对误差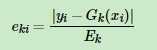，每个样本的相对误差加权求和得到这个基学习器的误差率e_k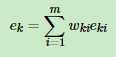

注意：

同样根据误差率更新基学习器权重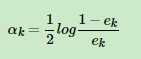，再更新样本权重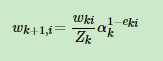：其中Z也是规范化因子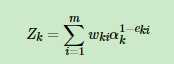

这里的公式这么理解：如果这个样本的误差率比较大，那么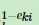就会比较小，由于a_k是一个小于1的数，所以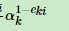这个就会比较大，同时样本权重就加大了，

3、最后也是通过训练出来的K个分类器进行决策：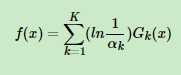

损失函数优化：

前面我们只是介绍了计算权重、系数的公式，没有解释原因，以下推导这个公式产生的原因

Adaboost是模型为加法模型，学习算法为前向分步学习算法，损失函数为指数函数的分类问题。

加法模型很好理解：因为我们最终决策是根据这K个决策树相加来做决策的

前向分步学习也很好理解：因为t+1轮学习期是根据t轮学习期的结果进行的

损失函数为指数函数：真是难理解这里

定义损失函数为：

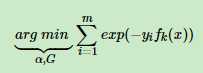这里这样理解：如果yi与预测值f（x）一致，那么想成是>0，那么指数就会比较小，比1小；如果yi与预测值f（x）不一致，那么想成是<0，加个负号大于0，指数就变大大于1，把所有的样本的这个指数值累加，如果能够取最小，说明都分类对了嘛，所以这个是他的损失函数，完美！！！

由于我们前面了解到了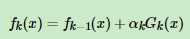，，所以代入得到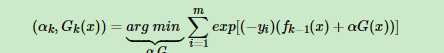

所以损失函数再变化成下面的样子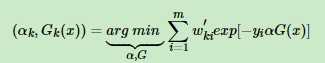

后面暂时还不理解。。。

 Adaboost算法正则化：

对于Adaboost算法我们也可以加入正则化，其实就是加在每个基分类器前面