2018-03-15 13:11:12
背包问题(Knapsack problem)是一种组合优化的NP完全问题。问题可以描述为:给定一组物品,每种物品都有自己的重量和价格,在限定的总重量内,我们如何选择,才能使得物品的总价格最高。问题的名称来源于如何选择最合适的物品放置于给定背包中。
相似问题经常出现在商业、组合数学,计算复杂性理论、密码学和应用数学等领域中。
一、0/1背包问题
背包问题是个NPC问题,01背包可以通过动态规划算法在伪多项式时间内给出解。
0/1背包问题的特点是,每种物品仅仅有一件,且需要选择放或者不放。
在0/1背包问题中,物品i或者被装入背包,或者不被装入背包,设xi表示物品i装入背包的情况,则当xi=0时,表示物品i没有被装入背包,xi=1时,表示物品i被装入背包。根据问题的要求,有如下约束条件和目标函数:
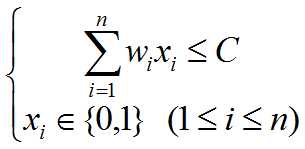
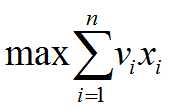
于是,问题归结为寻找一个满足约束条件式2.1,并使目标函数式2.2达到最大的解向量X=(x1, x2, …, xn)。
0/1背包问题可以看作是决策一个序列(x1, x2, …, xn),对任一变量xi的决策是决定xi=1还是xi=0。在对xi-1决策后,已确定了(x1, …, xi-1),在决策xi时,问题处于下列两种状态之一:
(1)背包容量不足以装入物品i,则xi=0,背包不增加价值;
(2)背包容量可以装入物品i,则xi=1,背包的价值增加了vi。
这两种情况下背包价值的最大者应该是对xi决策后的背包价值。令V(i, j)表示在前i(1≤i≤n)个物品中能够装入容量为j(1≤j≤C)的背包中的物品的最大值,则可以得到如下动态规划函数:
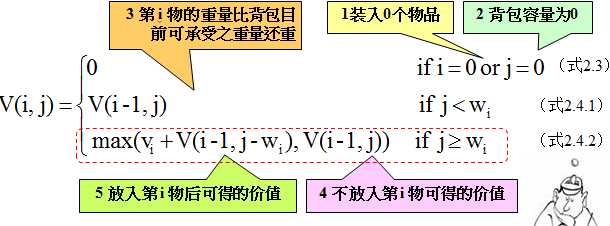
式2.3表明:把前面i个物品装入容量为0的背包和把0个物品装入容量为j的背包,得到的价值均为0。
式2.4的第一个式子表明:如果第i个物品的重量大于背包的容量,则装入前i个物品得到的最大价值和装入前i-1个物品得到的最大价值是相同的,即物品i不能装入背包;第二个式子表明:如果第i个物品的重量小于背包的容量,则会有以下两种情况:
(1)如果把第i个物品装入背包,则背包中物品的价值等于把前i-1个物品装入容量为j-wi的背包中的价值加上第i个物品的价值vi;
(2)如果第i个物品没有装入背包,则背包中物品的价值就等于把前i-1个物品装入容量为j的背包中所取得的价值。显然,取二者中价值较大者作为把前i个物品装入容量为j的背包中的最优解。
举个例子:
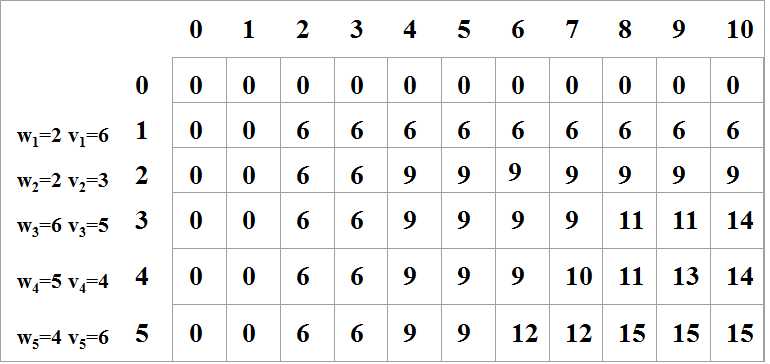
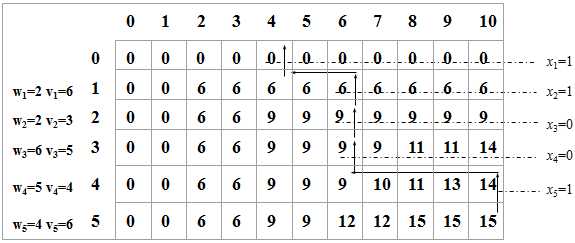
例如,有5个物品,其重量分别是{2, 2, 6, 5, 4},价值分别为{6, 3, 5, 4, 6},背包的容量为10。
根据动态规划函数,用一个(n+1)×(C+1)的二维表V,V[i][j]表示把前i个物品装入容量为j的背包中获得的最大价值。
第一阶段,只装入前1个物品,确定在各种情况下的背包能够得到的最大价值;
第二阶段,只装入前2个物品,确定在各种情况下的背包能够得到的最大价值;
依此类推,直到第n个阶段。最后,V(n,C)便是在容量为C的背包中装入n个物品
时取得的最大价值。
如何确定装入背包的具体物品?
从V(n,C)的值向前推,如果V(n,C)>V(n-1,C),表明第n个物品被装入背包,前n-1个物品被装入容量为C-wn的背包中;否则,第n个物品没有被装入背包,前n-1个物品被装入容量为C的背包中。依此类推,直到确定第1个物品是否被装入背包中为止。由此,得到如下函数:
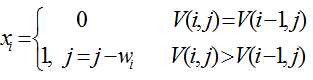
public class Knapsack {
static int knapsack(int[] v, int[] w, int W) {
int n = v.length;
int[][] V = new int[n + 1][W + 1];
int[] x = new int[n + 1];
for (int i = 0; i < W + 1; i++) {
V[0][i] = 0;
}
for (int i = 0; i < n + 1; i++) {
V[i][0] = 0;
}
for (int i = 1; i <= n; i++) {
for (int j = 1; j <= W; j++) {
if (j < w[i - 1]) V[i][j] = V[i - 1][j];
else V[i][j] = Math.max(V[i - 1][j - w[i - 1]] + v[i - 1], V[i - 1][j]);
}
}
int j = W;
for (int i = n; i >= 1; i--) {
if (V[i][j] == V[i - 1][j]) x[i] = 0;
else {
j -= w[i - 1];
x[i] = 1;
}
}
for (int i = 1; i <= n; i++) {
System.out.println(x[i]);
}
return V[n][W];
}
public static void main(String[] args) {
System.out.println(knapsack(new int[]{6, 3, 5, 4, 6}, new int[]{2, 2, 6, 5, 4}, 10));
}
}
相关的优化处理:
时间复杂度已经无法进一步进行优化了,但是空间复杂度还是有优化余地的,通过递推式可以看到,每次下一行的值的产生仅仅依赖于上一行的前面两个值,因此,我们可以将二维数组优化成一维数组进行存储。
static int polish(int[] v, int[] w, int W){
int n = v.length;
int[] m = new int[W + 1];
m[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = W; j >= w[i - 1]; j--) {
m[j] = Math.max(m[j - w[i - 1]] + v[i - 1], m[j]);
}
}
return m[W];
}
另外,在初始化的时候,如果是题目没有要求必须得最终装满背包,则直接使用上述代码即可,如果题目中指出必须装满背包,则在初始化的时候,除了V[0][0] = 0外,其余的0件物品,j个重量,抑或j个重量,0件物品都是不满足装满背包的条件的,应该初始化为负无穷大。
二、完全背包问题
完全背包问题同样给出了n件物品的重量和价值,并且给出了背包的大小W,但是和0/1背包不同的是,在完全背包问题中,每件物品可以选1,2,3...直到背包放不下为止。
完全背包是0/1背包问题的一个扩展,也同样是一个非常经典的问题。
运用类比的思想,我们可以将完全背包转化成0/1背包,具体的转化可以有下面两种方式:
1、将每件物品看成W/w[i]件,价值不变;
2、将每件物品看成v[i]*2^k,重量为w[i]*2^k,想法就是利用二进制的角度看问题,任何多种选择都可以通过这些二进制数相加得到,这种方法的分解个数显然要小很多,非常聪明。
如果从递推式的角度来解决问题,可以得到一个非常好的解答:
V[i][j] = max{V[i - 1][j], V[i][j - w[i]] + v[i]}
对于每一个V[i][j]都可以看成要么不选择第i件,要么选择第i件且可以多选,那么就可以很容易的得到上述的递推式。
下面使用一维数组进行实现,你会发现除了内层的顺序变了,其他的都没有改变。
static int polish(int[] v, int[] w, int W){
int n = v.length;
int[] m = new int[W + 1];
m[0] = 0;
for (int i = 1; i <= n; i++) {
for (int j = w[i - 1]; j <= W; j--) {
m[j] = Math.max(m[j - w[i - 1]] + v[i - 1], m[j]);
}
}
return m[W];
}
