发现自己学的一直都是假的ST表QWQ。
ST表
ST表的功能很简单
它是解决RMQ问题(区间最值问题)的一种强有力的工具
它可以做到$O(nlogn)$预处理,$O(1)$查询最值
算法
ST表是利用的是倍增的思想
拿最大值来说
我们用$Max[i][j]$表示,从$i$位置开始的$2^j$个数中的最大值,例如$Max[i][1]$表示的是$i$位置和$i+1$位置中两个数的最大值
那么转移的时候我们可以把当前区间拆成两个区间并分别取最大值(注意这里的编号是从$1$开始的)

查询的时候也比较简单
我们计算出$log_2{(区间长度)}$
然后对于左端点和右端点分别进行查询,这样可以保证一定可以覆盖查询的区间
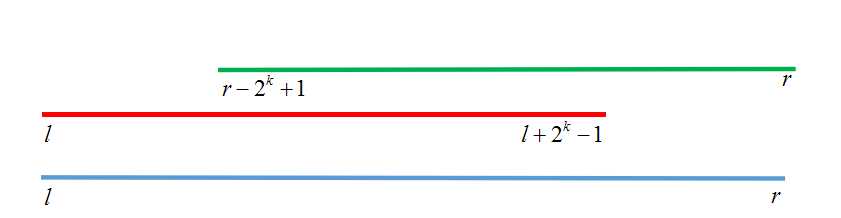
刚开始学的时候我不太理解为什么从右端点开始查的时候左端点是$r-2^k+1$
实际很简单,因为我们需要找到一个点$x$,使得$x+2^k-1=r$
这样的话就可以得到$x=r-2^k+1$
上面讲的可能比较抽象,建议大家画个图好好理解一下
代码
有了上面的知识,代码就比较好理解了
#include<cstdio> #include<cmath> #include<algorithm> using namespace std; const int MAXN=1e6+10; inline int read() { char c=getchar();int x=0,f=1; while(c<‘0‘||c>‘9‘){if(c==‘-‘)f=-1;c=getchar();} while(c>=‘0‘&&c<=‘9‘){x=x*10+c-‘0‘;c=getchar();} return x*f; } int Max[MAXN][21]; int Query(int l,int r) { int k=log2(r-l+1); return max(Max[l][k],Max[r-(1<<k)+1][k]);//把拆出来的区间分别取最值 } int main() { #ifdef WIN32 freopen("a.in","r",stdin); #endif int N=read(),M=read(); for(int i=1;i<=N;i++) Max[i][0]=read(); for(int j=1;j<=21;j++) for(int i=1;i+(1<<j)-1<=N;i++)//注意这里要控制边界 Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);//如果看不懂边界的话建议好好看看图 for(int i=1;i<=M;i++) { int l=read(),r=read(); printf("%d\n",Query(l,r)); } return 0; }
