2018-03-17 14:58:38
问题描述:已知一个2维矩阵,其中的元素每一行从左至右依次增加,每一列从上到下依次增加。即对于矩阵Table有Table[i][j] ≤Table[i][j + 1], Table[i][j] ≤ Table[i + 1][j],我们也称这样的矩阵为杨氏矩阵。给出判定某个数是否存在该矩阵中的高效算法。
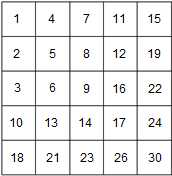
问题求解:这个题目个人感觉非常有意思,第一眼看过去会有一种二分查找的二维推广的感觉,似乎可以用二分查找的方法来解决。这里不妨假设矩阵的规模为n * n。
如果采用每行的二分查找算法的话,那么算法的时间复杂度无疑是O(nlogn),还是比较大的。那如何采用一种方法更有效的利用好这里的已排序的信息呢?
事实上,可以采用Step-wise进行线性搜索,也就是使用步进的方式进行查找,最终可以在O(n)的时间复杂度内完成查找。
思路理解起来也并不困难,就是从矩阵的右上角开始查找,不妨设其为m,如果待查找的值x小于m,则删去一列,如果待查找的值x大于m,则删去一行。
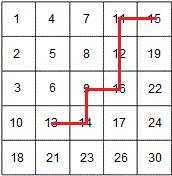
如下图显示了查找13的轨迹。首先与右上角15比较,13<15,所以去掉最右1列,然后与11比较,这是13>11,去掉最上面1行…以此类推,最后找到13。算法复杂度O(n),最坏情况需要2n步,即从右上角开始查找,而要查找的目标值在左下角的时候。
boolean stepwise(int[][] m, int target) {
int row = m.length;
int col = m[0].length;
int x = 0;
int y = col - 1;
while (x < row && y >= 0) {
if (target > m[x][y])
x++;
else if (target < m[x][y])
y--;
else return true;
}
return false;
}
