0 为什么会有多叉树
当在程序中存储数据的时候,可以使用二叉搜索树。
当输入的过于均匀的时候可能生成深度过大的二叉搜索树,最坏的情况是,输入节点的key按照大小排序,此时生成的二叉搜索树就是一个链表了。
因此,为了避免这种情况的出现,可以使用平衡二叉树,例如AVL和红黑树。
但二叉搜索树只是适用于数据存储在内存中的情况。
当数据量过大,不能完全的在内存中存储时,就需要将数据存储到磁盘上。
为了检索方便,仍然使用树的结构。
如果存放在磁盘中的数据,仍然采用二叉搜索树的形式,当磁盘中读取出一块数据,根据key的值,判断目标应该在左子树中,然后磁盘再去读取左子树数据所在磁盘位置的数据。然后迭代这个过程,直到找到了目标数据。
但是,磁盘每次读取数据都需要一定的时间。因此树高越大,那么平均读取依次数据需要读取的磁盘次数也就越多。
cpu的计算速度远快与磁盘读取的次数,因此应该减少树高,降低磁盘的读取次数。
所以在每个节点中除了本节点key对应的值,再存储多个子树。而不是像二叉搜索树,只存放左右子节点。
此时该结构就是B树
2 B树
2.1 结构
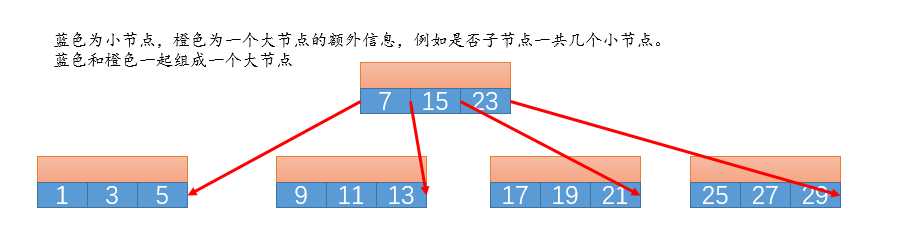
B树的每个节点存放:
- 一个数值n,表示该节点中存在的节点个数。
- n个节点本身,按照节点关键字非降序存放(也就是从小打到),这n个节点的关键字,分割了本节点的n个子树中key的取值范围。
- 一个布尔值,表示概述是否是一个叶节点
- n+1个指针指向每一个子树,取值范围被n个关键字分割
注意:父节点的指针在子树中的指向。
2.2 特点
B树具有
- 每个叶节点的树高相同
- 每个节点所包含关键字个数有上下界。称为B树的最小度数。用t表示,一个大节点中小节点的个数最少为t-1个,最多为2t-1,其子树数量最多为2t个。因此当t=2时,为2-3-4树。t越大,树高越小
- B树的根至少包含一个子树,其他节点至少有t个子树
2.3 搜索
B树的根节点时钟在主存中。
搜索过程:
Node *serch(Node *root,int k)
{
int i=0;
for(;i<=root.n,k>x.key[i],++i)
{
}
if(k==x.key[i])
{
return x.child[i];
}else if(x.leaf == true)
{
return nullptr;
}else{
return serch(read(x.key),k);
}
}
2.4 插入
B树的插入,B树的插入仍然和二叉树的插入步骤类似,也就是说都要先判断插入位置。
但是多了一个判断:那么就是一个节点中可存储的节点个数,不能超过2t。当超过2t个的时候,需要这样做。
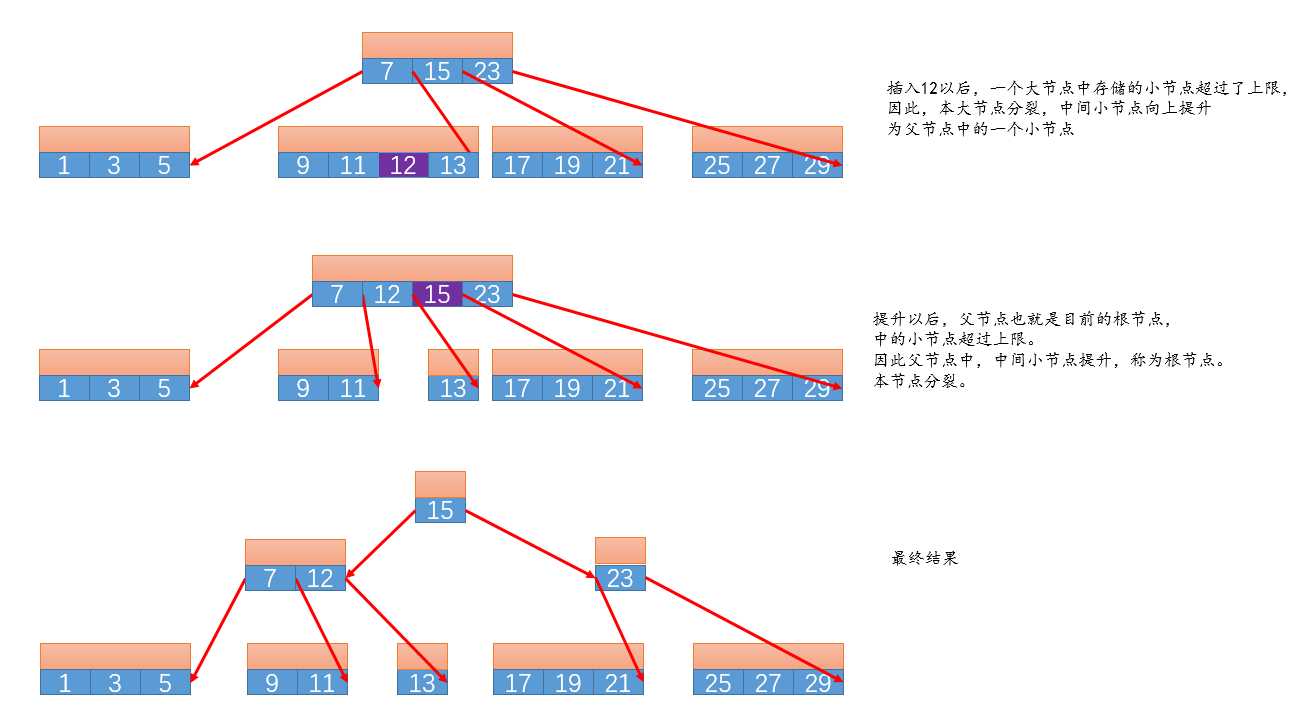
- 遍历找到要插入的位置。
- 判断大节点中小节点的个数,如果为2t。那么用本大节点中的中间节点将小结一分为二,将第n/2+1个节点上升到父节点。
- 如果父节点中小节点的个数也为2t了,那么父节点重复上述分裂过程
2.5 删除
删除节点过程:
- 每次删除一个节点的时候,都需要判断该节点的父节点,叔叔节点,祖父节点中的子节点个数。如果删除目标节点以后,父节点,叔叔节点,祖父节点的小节点个数满足<=2t那么合并这三个节点为一个节点
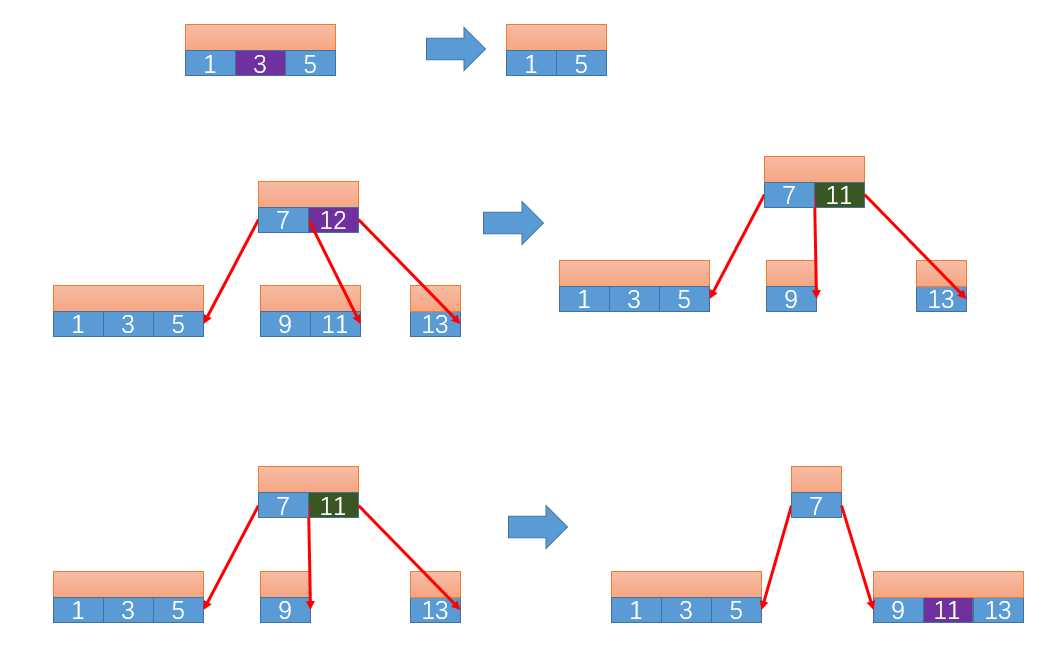
- 具体的删除每个节点的策略:
- 当目标小节点是位于所有小节点中间的时候,那么就合并该小节点两边指向的两个子节点。
- 当目标小节点是所有小节点之后的节点的时候,那么就从该节点指出的两个子树的节点中选出一个大于t的节点,然后将其换到目标节点处。如果都不够,那么先合并两个子节点,然后提出中间节点。
下面是三种删除的情况,只有两层,没有三层。
3 B+树
